band brasil
band USA
band espanha




circprob54-2J.jpg
Figura 54-02.1

    Note que o paralelo formado por R e XL, impedância denominada de ZL, formam um circuito com predominância indutiva. Com isso, sabe-se que I1 estará atrasada em relação à I2. E como IT é a soma fasorial entre I1 e I2, conclui-se que os valores destes três fasores formam os lados de um triângulo, conforme se pode ver na Figura 54-02.2.

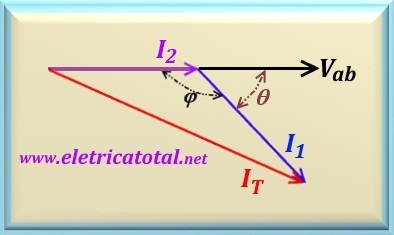
grafdif54-2J.jpg
Figura 54-02.2

    Como se conhece os três lados do triângulo, pode-se calcular o ângulo φ utilizando a lei dos cossenos. Então:

    cos φ = (I12 + I22 - IT2) / 2 I1 I2

    Fazendo a substituição pelos valores numéricos e efetuando-se o cálculo:

    cos φ = - 0,65       ⇒       φ = 130,54°

    A partir deste dado se pode calcular o valor do ângulo θ, que é dado por:

    θ = φ - 180° = 130,54° - 180°   ⇒   θ = - 49,46°

    Repare que se usou a convenção onde fasores abaixo do eixo horizontal devem ter ângulos negativos. Então, I1 = 18 ∠-49,46°. Agora é possível calcular a impedância do circuito paralelo, ZL.

    ZL = Vab / I1 = 60 ∠0° / 18 ∠-49,46° = 3,33∠+49,46°

    Por outro lado, pode-se escrever a admitância complexa para ZL, ou:

    YL = 1 / 3,33∠+49,46° = 0,195 - j0,228   S

    Portanto, calculando o inverso dos valores obtém-se:

    R = 1 / 0,195 = 5,13 Ω
    XL = 1 / 0,228 = 4,39 Ω