Problema 15-9 Fonte:
Problema elaborado pelo autor do site.
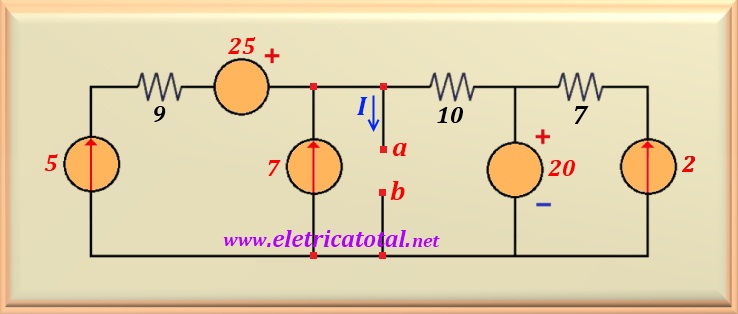
Determine o valor de I que circula entre os pontos a e b no circuito
mostrado na Figura 15-09.1, quando entre esses pontos são inseridos, alternadamente, resistores de valores
iguais a 4, 10 e 25 ohms. Além disso, calcule a potência dissipada em cada
resistor.
Solução do Problema 15-9 -
Método Thévenin/Norton
Pelo circuito percebemos que a fonte de corrente de 5 A está em série com o resistor
de 9 ohms e a fonte de tensão de 25 volts. Portanto, podemos eliminar estes dois últimos
componentes, já que estão em série com a fonte de corrente. E como sabemos, neste caso, a fonte de
corrente predomina. Desta forma, ficamos com as duas fontes de corrente em paralelo. Por outro lado, o
resistor de 7 ohms e a fonte de corrente de 2 A que está em série com ele, também podem ser eliminados do circuito, pois estão em paralelo com a fonte de tensão de 20 volts. Assim, ficamos
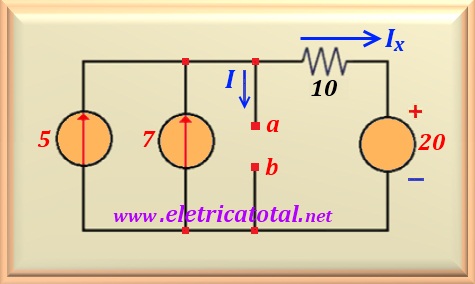
com o circuito simplificado mostrado na Figura 15-09.2.
Pelo circuito mostrado na figura acima, I = 0. Logo Ix = 7 + 5 = 12 A.
De posse destes dados, facilmente calculamos a tensão a circuito aberto nos pontos a-b, que representa a tensão de Thévenin para esse circuito.
E para determinarmos Rth, basta eliminarmos as fontes de corrente e
curto-circuitarmos a fonte de tensão. Assim, sobra o único resistor do circuito, logo:
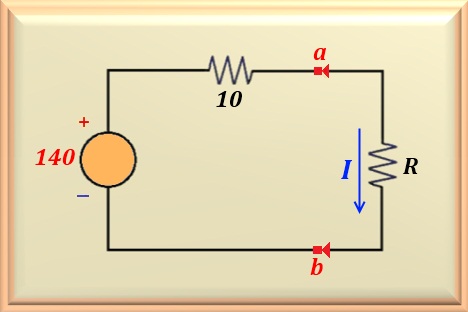
Na Figura 15-09.3, podemos apreciar o equivalente Thévenin do circuito. Note que entre os
pontos a-b foi colocado o resistor R que assumirá os valores do enunciado do
problema.
Quando R = 4 ohms a corrente I que circulará pelo circuito será:
E a potência dissipada por essa resistência será de:
Quando R = 10 ohms a corrente I que circulará pelo circuito será:
E a potência dissipada por essa resistência será de:
Quando R = 25 ohms a corrente I que circulará pelo circuito será:
E a potência dissipada por essa resistência será de:
Note como o resultado deste problema está em perfeita concordância com o
teorema da Máxima Transferência de Potência.