Este método, também conhecido como Deslocamento de Fontes, em análise de circuitos elétricos mostra-se extremamente útil quando temos um circuito com alguma complexidade, e através de transformação de fontes conseguimos simplificá-lo a ponto de torná-lo fácil de compreendê-lo para encontrar sua solução.

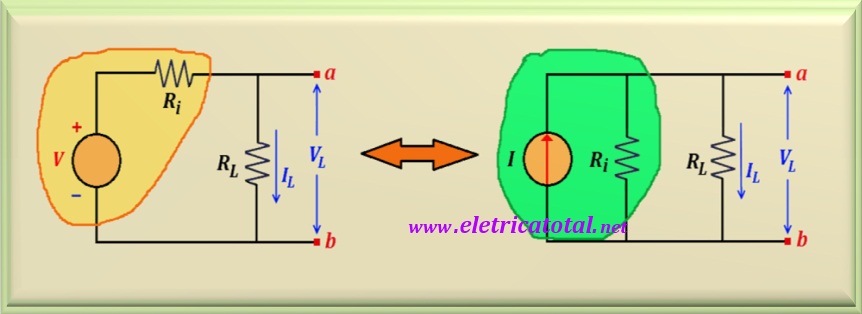
Devemos ter em mente que duas fontes são equivalentes se fornecem a mesma tensão de circuito aberto e a mesma corrente de curto-circuito. Apresentamos, na Figura 11-01 a equivalência que podemos ter entre os dois circuitos mostrados.

O que o circuito nos mostra é que sempre que tivermos uma fonte de tensão em SÉRIE com um resistor, podemos transformá-lo em uma fonte de corrente em PARALELO com o resistor. Devemos manter o valor do resistor. O valor da fonte de corrente é dado pela divisão entre o valor da fonte de tensão e o valor do resistor.

O mais interessante é que este processo é REVERSÍVEL. Em outras palavras: se tivermos uma fonte de corrente em PARALELO com um resistor, podemos transformá-lo em uma fonte de tensão em SÉRIE com o resistor. Também devemos manter o valor do resistor. O valor da fonte de tensão será dado pelo produto do valor da fonte de corrente e o valor do resistor. Fique atento para o fato que nestas transformações, o valor do resistor NUNCA se altera.

Porém, NÃO ESQUEÇA que se o resistor estiver em paralelo com a fonte de tensão não podemos fazer essa transformação. Na verdade, o que devemos fazer é eliminá-lo do circuito, pois sua ausência não altera em nada a solução do problema. Da mesma forma devemos agir caso o resistor esteja em série com uma fonte de corrente. Não podemos fazer a transformação acima, mas podemos eliminá-lo do circuito, pois também não alterará a solução do problema.

Vamos analisar como solucionar um circuito como o mostrado na Figura 11-02.

Como dito anteriormente, o resistor de valor igual a 8 ohms, que está em paralelo com a fonte de tensão de 12 volts, pode ser retirado do circuito sem prejuízo para a solução do problema. Além disso, repare que no circuito (figura acima) temos duas fontes de tensão em série com resistores. Logo, é perfeitamente possível realizarmos transformação de fontes. A fonte de tensão de 12 volts será transformada em uma fonte de corrente de 12 / 6 = 2 A em paralelo com o resistor de 6 ohms. Por sua vez, a fonte de tensão de 36 volts será transformada em uma fonte de corrente de 36 / 12 = 3 A em paralelo com o resistor de 12 ohms. Note o sentido da seta das fontes de corrente. A fonte de 2 A aponta para baixo, pois o pólo positivo da fonte de tensão de 12 volts apontava para baixo. Mesmo raciocínio aplica-se para a outra fonte de corrente. Veja na Figura 11-03 como ficou a nova configuração do circuito.

No circuito mostrado na Figura 11-03 percebemos que temos duas fontes de corrente em paralelo e com sentidos contrários. Logo, podemos transformá-las em uma única fonte de corrente de valor igual a subtração de seus valores, ou seja, 3 - 2 = 1 A. A seta da fonte de corrente aponta no sentido daquela que possui o maior valor numérico.

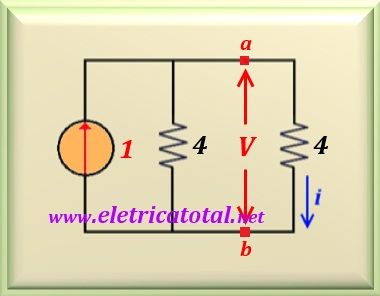
Por outro lado, à esquerda dos pontos a-b temos dois resistores em paralelo. Como resultado obtemos um único resistor de valor igual a 4 ohms. Veja na Figura 11-04 como ficou o circuito após as transformações.

Veja como simplificamos o circuito tornando fácil sua solução. Para calcularmos a corrente i podemos aplicar um divisor de corrente resistivo. Mas como os dois resistores tem valores iguais, naturalmente que circulará a metade da corrente da fonte de 1 A por cada resistor. Logo:

E aplicando-se a lei de Ohm podemos calcular a tensão V entre os pontos a - b. Assim:

Do mostrado acima, percebe-se que este método de resolução é muito rápido para encontrar a solução de problemas.