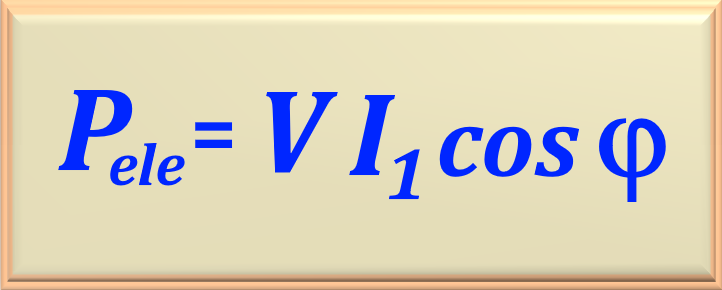Problema 108-10    Fonte:  Problema elaborado pelos autores do site.

O projeto de um motor de fase dividida, 127 V, com potência nominal de 1 HP, deve ter um rendimento de 68% e FP = 0,80. Além disso, deve possuir os seguintes parâmetros do circuito equivalente:

Z_P = 8,0 + j 5,5 Ω  Z_R = 0,8 + j 0,7 Ω

O motor deve funcionar com tensão e frequência nominais e o enrolamento auxiliar aberto. Sabe-se que as perdas no núcleo devem ser 40 W, as perdas rotacionais e suplementares 12,4 W. Determine:

a) a corrente de estator;

b) o valor da resistência R₁ do enrolamento principal;

c) o valor da reatância X₁ do enrolamento principal.

Solução do Problema 108-10   

Item a

Como é fornecida a potência nominal e o rendimento do motor, então usando a eq. 108-31, é possível calcular a potência de entrada do motor.

Para calcularmos a corrente elétrica no motor, vamos usar a eq. 108- 29, mostrada abaixo.

Depois de um trabalho algébrico, substituindo as variáveis por seus respectivos valores numéricos e efetuando o cálculo, obtemos:

Como FP = 0,8, podemos determinar o ângulo de atraso da corrente em relação à tensão aplicada ao motor, pois arccos 0,8 = ± 36,87° . E, como o circuito é indutivo, ou seja, o fator de potência é atrasado, então podemos escrever o valor fasorial de I₁ como:

Item b

Com o valor de V = 127 V e I₁ = 10,8∠ - 36,87° A, é possível calcular a impedância total do motor, apenas aplicando a lei de Ohm, ou seja:

É importante entender que o valor 9,4 Ω representa o valor da resistência total, R_total, do enrolamento principal. Como conhecemos o valor de R_P = 8,0 Ω e R_R = 0,8 Ω, facilmente calculamos o valor de R₁, pois sabemos que:

Assim, fazendo a substituição numérica nas variáveis e efetuando o cálculo, encontramos:

Item c

Para encontrarmos o valor de X₁, usamos a mesma linha de raciocínio do item anterior. Assim, temos X_total = 7,1 Ω e, sabemos que:

Fazendo a substituição numérica nas variáveis e efetuando o cálculo, obtemos: