Problema 52-7    Fonte:  Adaptado do Problema 12.17 - página 262 -    EDMINISTER, Joseph A. -    Livro: Circuitos Elétricos - Ed. McGraw Hill - 1971.

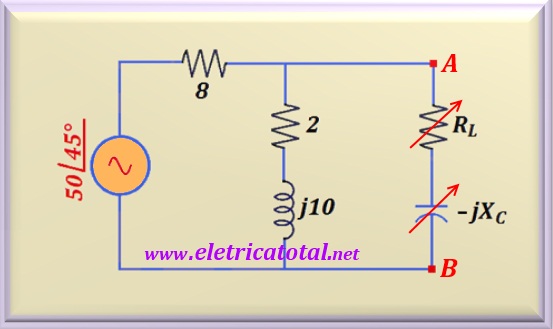
No circuito mostrado na mostrado na Figura 52-07.1, a carga ligada aos terminais A-B é constituída por um resistor variável R_L e uma reatância capacitiva X_C, variável entre 2 e 8 ohms. Determine o valor de R_L e X_C que acarretam a máxima transferência de potência à carga. Determine o valor dessa potência máxima fornecida à carga.

Solução do Problema 52-7   

Inicialmente, deve-se calcular o equivalente Thévenin do circuito.

Note que a impedância Z = 2 + j10 fica conectada em paralelo com o resistor de 8 ohms, quando se curto-circuita a fonte de tensão com o objetivo de calcular o equivalente Thévenin. Assim:

Efetuando-se o cálculo, obtém-se:

Para calcular a tensão de Thévenin, necessita-se calcular a tensão em circuito aberto nos pontos A-B. Usando um divisor de tensão:

Efetuando o cálculo, encontra-se:

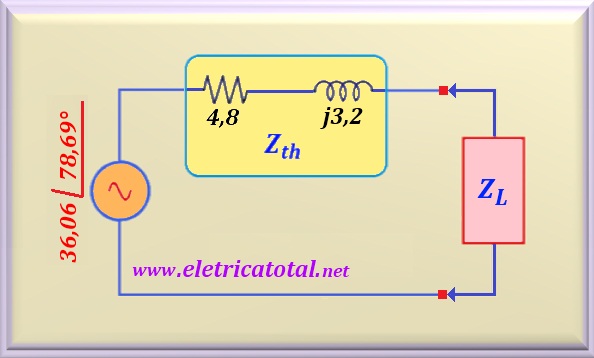
Com o cálculo do equivalente de Thévenin há condições de atender às solicitações do problema. Veja na Figura 52-07.2, o circuito que será usado na solução do problema.

Na figura acima, denominamos a carga composta por R_L e X_C por Z_L, ou seja, impedância da carga. Esta situação se remete ao caso 2 quando se estudou o teorema da máxima transferência de potência. Imediatamente, deduz-se que o valor de R_L deve ser igual ao valor de R_th, ou R_L = 4,8 Ω. Além disso, a seguinte condição deve ser satisfeita:

Ou seja, a carga deve ser o complexo conjugado de Z_th. Logo, o valor da reatância capacitiva deve ter um valor que anule a reatância indutiva de Z_th. Sendo assim, todo o circuito será representado por uma impedância puramente resistiva. Para que isso aconteça, deve-se ter: