Problema 15-13    Fuente:    Problema elaborado por el autor del sitio.

Basado en el problema anterior, considerando el circuito que se muestra en la Figura 15-13.1, determine a qué valor de R se produce la máxima disipación de potencia.

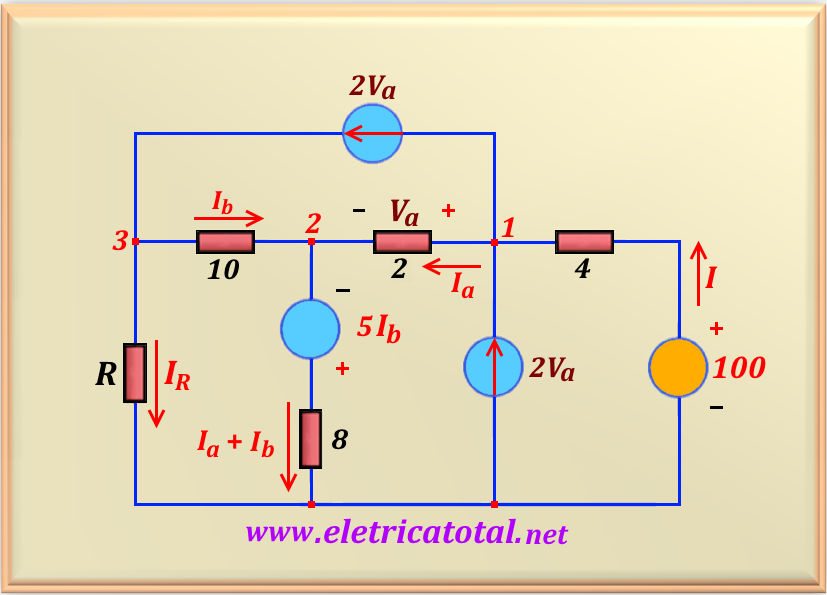
Solución del Problema 15-13

Nota que ya determinamos en el problema anterior que I = I_a. Por lo tanto, resolveremos usando como variable la corriente I . Entonces, concluimos que V_a = 2 I, y que la fuente de corriente 2 V_a = 4 I. Entonces podemos escribir eso I_R = 4 I - I_b. Después de estas consideraciones y en base al circuito que se muestra en la Figura 15-13.1 , hagamos la malla indicada por la flecha naranja. Así:

Reorganizando algebraicamente la ecuación anterior, encontraremos una relación entre I y I_b. Así:

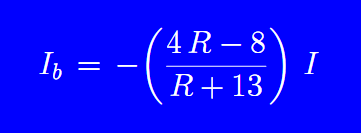
Como I_R = 4 I - I_b, reemplazando I_b con la ecuación anterior y realizando una manipulación algebraica encontramos:

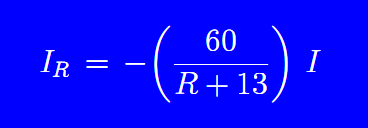
Conociendo el valor de I_R, podemos calcular la potencia disipada por R y luego calcular el valor de R para obtener la potencia máxima disipada por ella. Esto requiere un conocimiento básico de Cálculo avanzado. Para aquellos que conocen este contenido, hemos preparado un artículo en PDF al que se puede acceder Click aquí!!!.  Pero podemos adelantar que el valor encontrado es:

Para confirmar este resultado, mostramos en la figura a continuación un gráfico, que se obtuvo de la ecuación de potencia disipada por la resistencia R dada por la expresión a continuación:

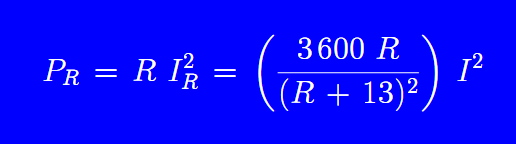
Al hacer un arreglo algebraico, obtenemos:

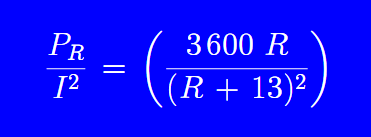
Entonces, al trazar esta ecuación en un programa como Geogebra, obtenemos la curva que se muestra en la figura a continuación. Tenga en cuenta que el gráfico muestra claramente que la potencia máxima disipada por R es cuando su valor es igual a R = 13 ohmios.