Problema 55-10
Fonte: Problema 13 - Lista de Problemas RLC - Disciplina
Circuitos Elétricos da Escola de Engenharia - UFRGS - 2011 - Prof. Dr. Valner Brusamarello.
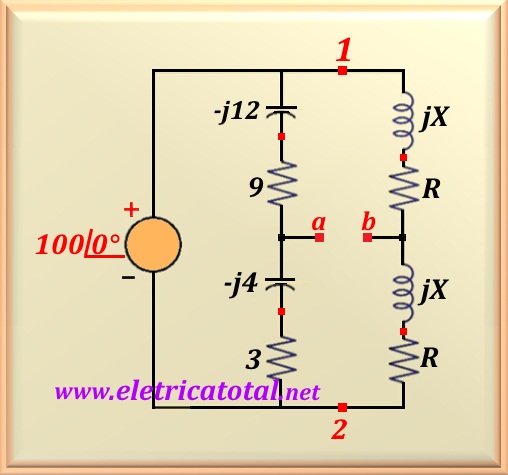
Determine Vab em módulo e fase conforme circuito mostrado na Figura 55-10.1.
Solução do Problema 55-10
Observe que é possível calcular a impedância do ramo 1-a-2 somando os valores dos componentes, pois estão conectados em série.
Logo, a impedância será:
Assim, conhecendo a impedância se pode calcular o valor de I1, ou:
Note que a impedância entre o ponto 1 e o ponto a é Z1a = 9 - j12 = 15∠-53,13°.
Dessa forma, pode-se calcular a tensão entre o ponto 1 e o ponto a, ou:
Sobre o ramo 1-b-2, note que a impedância entre os pontos 1-b e b-2 são exatamente iguais,
independente dos valores de R e X. Isso implica que
V1b = Vb2. E como a tensão da fonte é V = 100∠0°, conclui-se que:
Para se encontrar o valor de Vab basta fazer a malha superior, ou:
Fazendo a substituição numérica e efetuando o cálculo:
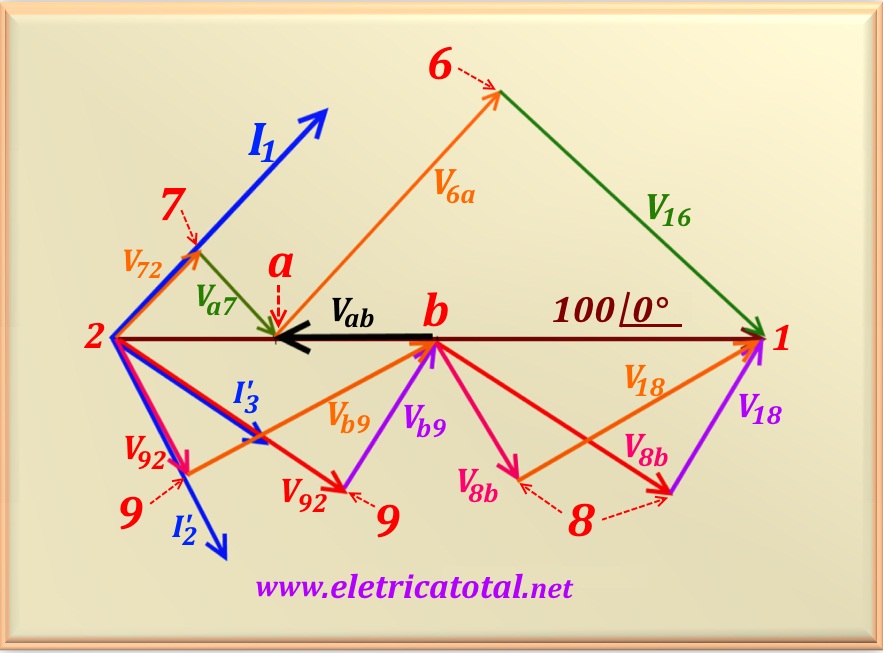
Na Figura 55-10.2, apresenta-se um diagrama fasorial das tensões e
correntes no circuito. Repare que os fasores que estão acima da tensão de referência são correspondentes ao ramo que contém capacitores. Vamos analisar o ramo que está entre os pontos 2 e a: note que a tensão V72
está em fase com a corrente I1 e é a tensão sobre o resistor de 3 ohms; a tensão
Va7 é a tensão sobre o capacitor -j3 e está atrasada de 90° em relação à tensão sobre o resistor, V72; a soma fasorial dessas duas tensões é a tensão Va2.
Agora, vamos analisar o ramo que está entre os pontos a e 1: a tensão V6a é a tensão sobre o resistor de 9 ohms e está em fase com I1 como se pode ver no diagrama; a tensão V16 é a tensão sobre o capacitor e está atrasada de 90° em relação à tensão sobre o resistor, V6a; a soma fasorial dessas duas tensões é a tensão V1a, cujo valor foi calculado e é igual a V1a = 75∠0°.
Agora vamos fazer uma análise da parte que se encontra abaixo da tensão de referência e, nesse caso, analisando o ramo que contém os indutores.
Para ficar evidente que a solução do problema é independente dos valores de R e XL,
optou-se por representar duas correntes, I'2 e I'3, com ângulos de fase diferentes, o que significa dois valores diferentes para R e XL. Repare que para o caso de I'3, resulta V92 > Vb9, logo R > XL. E para I'2, resulta V92 < Vb9, logo R < XL. Verifica-se então que, para quaisquer valores de R e XL se obtém a mesma solução para Vab.
Veja, no diagrama, Vab apontando em sentido contrário ao da tensão da fonte de alimentação.
Isto justifica o valor encontrado Vab = -25∠0° = 25 ∠180° V.