Problema 13-8 Fonte:
Questão 27 - UFSC - Concurso Público- Edital 172/DDP/2014
- Cargo/Área de Especialização: Técnico em Eletrotécnica.
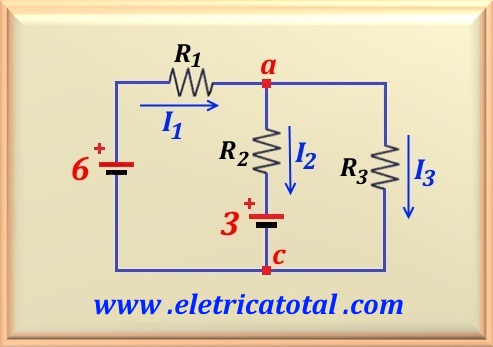
O circuito mostrado na Figura 13-08.1 é composto por três resistores – R1 , R2 e R3 – e duas fontes de tensão contínuas –
E1 e E2. Sabendo que:
R1 = 2 Ω, R2 = 1 Ω, R3 = 1 Ω,
E1 = 6 volts e E2 = 3 volts.
Analise as seguintes alternativas:
I. A corrente I1 tem intensidade 3A.
II. A corrente I2 tem intensidade 3A.
III. A corrente I3 tem intensidade -6A.
IV. A corrente I2 tem sentido inverso ao mostrado na figura.
V. A potência consumida em todos os resistores é de 54W.
VI. A diferença de potencial elétrico sobre o resistor R1 é de 6V.
VII. A diferença de potencial elétrico sobre o resistor R2 é de 4V.
VIII. A diferença de potencial elétrico sobre o resistor R3 é de 3V.
Assinale a alternativa CORRETA.
A ( ) Somente as afirmativas II, V, VI e VIII são corretas.
B ( ) Somente as afirmativas I, II, V e VI são corretas.
C ( ) Somente as afirmativas I, IV, V e VI são corretas.
D ( ) Somente as afirmativas III, IV, VII e VIII são corretas.
E ( ) Somente as afirmativas II, IV, V e VI são corretas.
Atenção - Nesta questão a única
afirmativa correta é a IV,
conforme pode ser comprovado na solução deste problema. Porém, nenhuma alternativa
contempla esta opção.
Portanto, não há alternativa correta. Houve um erro na elaboração da questão e ela
provavelmente foi anulada.
Solução do Problema 13-8 -
Método Kirchhoff
Inicialmente podemos escrever a equação para o nó a, onde temos a
concorrência das três
correntes que aparecem no circuito. Assim:
Como há três incógnitas no problema, então há necessidade de três equações para a solução do mesmo.
Vamos escrever as outras duas equações. Começando pelo ponto c e percorrendo a fonte de tensão de 6 volts temos:
Para encontrarmos a terceira equação vamos começar no ponto c e percorrer a fonte de tensão de 3 volts, ou:
Substituindo o valor de I3, nesta última equação, pelo valor encontrado na primeira equação, obtemos:
Rearranjando estas equações chegamos a um sistema de duas equações a duas incógnitas, conforme abaixo:
Resolvendo este sistema por qualquer método, obtem-se:
Agora substituindo estes valores na primeira equação, encontra-se o valor de I3, ou:
De posse destes valores podemos calcular as quedas de tensão em todos os resistores, ou: