Problema 11-7 Fonte:
Prob. 34 - página 114 - HAYT, William H. Jr. ,
KEMMERLY, Jack E. , DURBIN, Steven M. - Livro: Análise de Circuitos em Engenharia -
Ed. McGraw Hill - 7ª Edição - 2008.
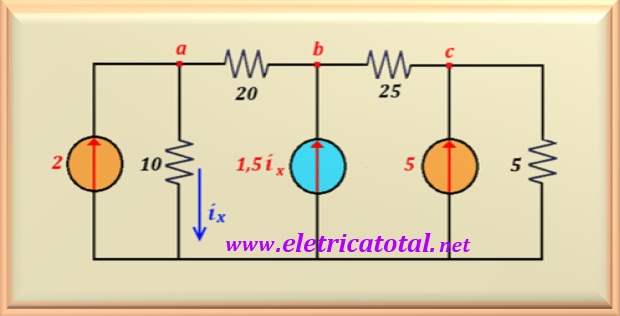
No circuito mostrado na Figura 11-07.1, calcule a corrente ix.
Solução do problema usando Tensão Nodal
clique aqui!
Solução do Problema 11-7 -
Transformação de Fontes
Vamos iniciar nossa análise fazendo uma transformação de fonte no lado direito da figura
acima. A transformação será entre a fonte de corrente
de 5 A e o resistor de 5 ohms que está em paralelo com a mesma.
Isto resultará em uma fonte de tensão de 25 volts e o resistor de 5 ohms
ficará em série com o outro resistor do circuito de valor igual a 25 ohms.
Como os dois estão em série então podemos somar seus valores resultando em
um resistor de 30 ohms em série com a fonte de tensão de 25 volts.
Dessa forma, podemos fazer uma nova transformação resultando em uma fonte de corrente
de 25/30 A em paralelo com o resistor de 30 ohms.
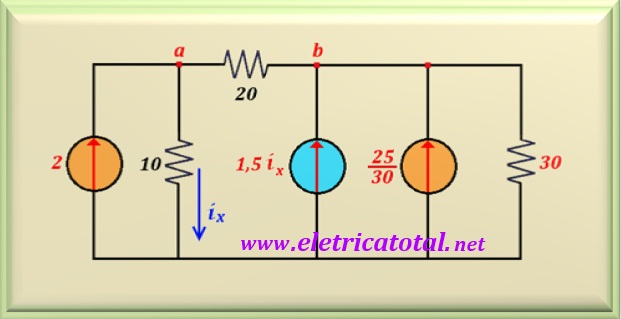
Na Figura 11-07.2 redesenhamos o circuito com as transformações aplicadas.
Como as duas fontes de corrente apontam no mesmo sentido podemos somá-las.
Então obtemos uma fonte de corrente de valor igual a 1,5 ix + (25/30).
Realizando mais uma transformação de fontes encontramos uma fonte de tensão de
45 ix + 25.
Os resistores de 20 e 30 ohms ficam em série e podemos substituí-los
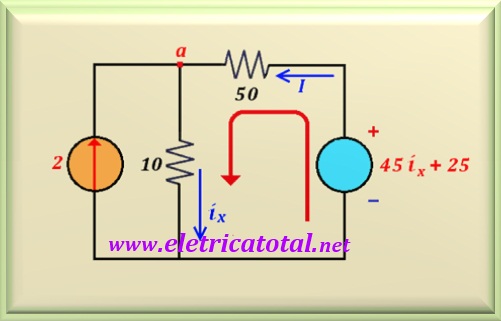
por um único de 20 + 30 = 50 ohms, resultando o circuito conforme
a Figura 11-07.3.
Repare que denominamos a corrente que circula pelo resistor de 50 ohms
de I. Logo, do circuito podemos escrever que:
Fazendo a equação de malha no sentido da seta vermelha, indicada na figura acima,
conseguimos a seguinte equação:
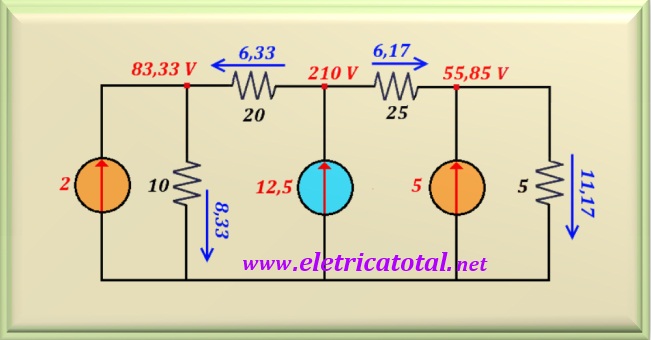
Substituindo o valor de I nesta última equação, facilmente encontramos o valor de
ix, cujo valor é: