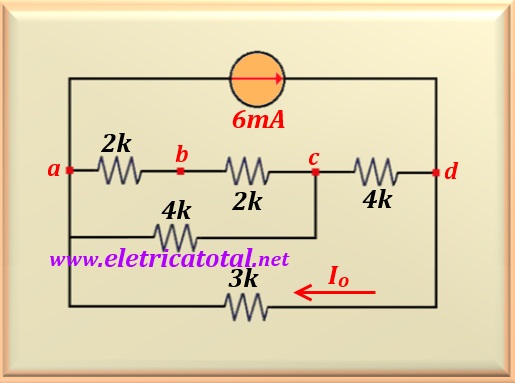
Problema 10.12 Fuente:
Problema 2.57 - página 74 - IRWIN, J. David - Libro: Análise de Circuitos em Engenharia - 4ª edição - Ed. Pearson Education do Brasil - 2013.
Determine el valor de Io en el circuito que se muestra en la
Figura 10-12.1.
Solución del Problema 10-12
Para comenzar a resolver este problema, los nodos recibirán nombres. Por lo tanto, está claro que
hay dos resistencias en paralelo entre los nodos a-b. Uno de 6 kΩ y uno de
3 kΩ. Resolver este paralelo da una resistencia equivalente de valor
igual a 2 kΩ. Entre los nodos c-d sucede lo mismo. Hay dos
resistencias en paralelo: una de 6 kΩ y otra de 12 kΩ.
Resolver este paralelo da una resistencia equivalente de 4 kΩ . Por
lo tanto, podemos simplificar el circuito como se muestra en la Figura 10-12.2.
Nota que en la rama a-b-c hay dos resistencias en serie de 2 kΩ
cada una. Por lo tanto, al sumar los dos, se obtiene una resistencia única de 4 kΩ.
Sin embargo, esta resistencia es paralela a la otra de 4 kΩ. Ahora
calcular el paralelo produce una resistencia única de 2 kΩ que
interconecta los nodos a-c, cómo vemos en la Figura 10-12.3.
Así, el circuito se redujo significativamente. Al encontrar el valor de la serie
de 2 y 4 kΩ, podemos calcular el valor de
Io (que da como resultado una resistencia de
6 kΩ). Se debe calcular el paralelo de las resistencias de
6 y 3 kΩ. Esto se origina una resistencia única de
2 kΩ entre los nodos a-d. Entonces, la diferencia potencial
entre los nodos d-a será:
Ahora, para encontrar el valor de Io simplemente aplique la Ley de Ohm:
Otra forma de encontrar el valor de Io, sin
necesita calcular Vda, sería aplicar un
divisor de corriente. Así: