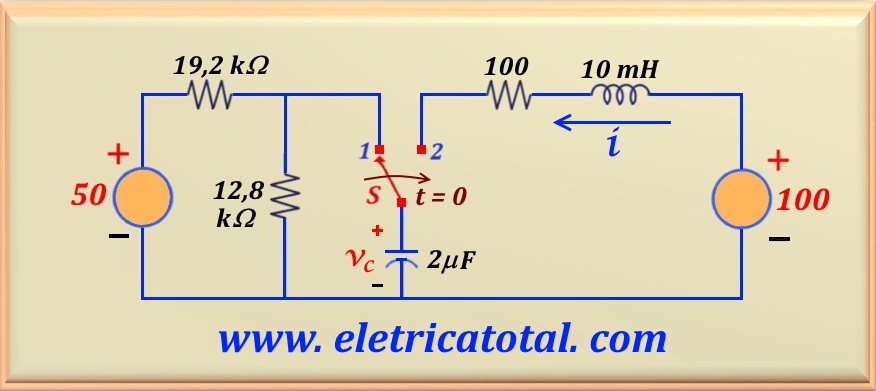
Problema 25-1    Fonte:   Exercício 8.7 - página 190 - NILSSON, James W. & RIEDEL, Susan A. - Livro: Circuitos Elétricos - Editora LTC - 5ª edição - 1999.

No circuito mostrado na Figura 25-1.1 abaixo, a chave S ficou na posição 1 por um longo período. Em t = 0 a chave é deslocada para a posição 2. Determine:

a) i (0⁺)

b) v_C(0⁺)

c) d i(0⁺) / d t

d) as raízes da equação característica que descreve o comportamento transiente do circuito.

Solução do Problema 25-1

Item a

Observe que enquanto a chave S esteve na posição 1 a corrente i era nula, pois o lado direito do circuito estava aberto. Então, quando passamos a chave para a posição 2, o indutor não pode mudar bruscamente seu valor. Logo, conclui-se que:

Item b

Enquanto a chave S esteve na posição 1, o capacitor foi carregado pela tensão sobre o resistor de 12,8 kΩ e está se comportando como um circuito aberto. Então podemos aplicar um divisor de tensão resistivo e calcular essa tensão. Logo:

Assim, quando passamos a chave S para a posição 2, o capacitor está carregado com essa tensão e como um capacitor não pode mudar sua tensão bruscamente, conclui-se que:

Item c

Como estudamos na parte teórica, a derivada da corrente no indutor é dada por:

Lembre-se que V_o é a tensão em cima do indutor em t = 0⁺. Nesse instante a corrente é nula, então V_o é a diferença entre a tensão da fonte e a tensão no capacitor. Ora, efetuando o cálculo temos V_o = 100 - 20 = 80 volts. Substituindo este valor na equação acima temos:

Item d

Usando a eq. 25-05 é possível calcular os valores de α e ω_o. Então:

Nesse circuito temos α < ω_o, pois ω_o = 7071 rad/s, caracterizando uma resposta subamortecida. Assim, as raízes são complexas e conjugadas. Por outro lado, pode-se calcular o valor de ω_d usando a eq. 25-12, ou:

Usando a eq. 25-11 como referência, pode-se escrever as raízes da equação característica como: