Problema 22-5 Fonte:
Problema 7.30 - página 300 Livro: Análise de Circuitos em Engenharia -
J. David Irwin - 4ª edição - Ed. Pearson - 2013.
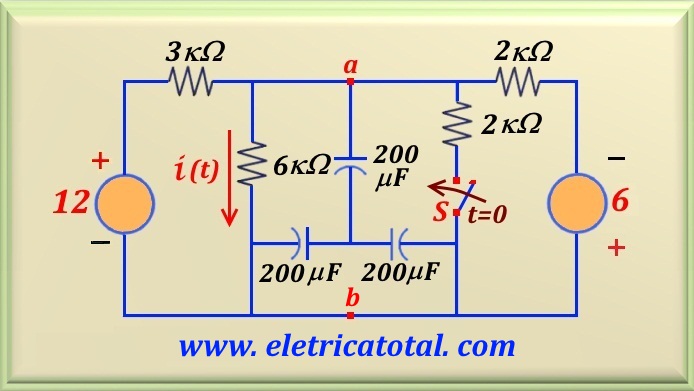
No circuito mostrado na Figura 22-05.1 abaixo, a chave S permaneceu aberta por um longo período de tempo.
Em t = 0 a chave S é fechada. Determine a corrente i (t).
Repare que temos uma associação de capacitores no circuito. Os dois de baixo estão
em paralelo, totalizando uma capacitância de 400 µF. Este por sua vez,
fica em série com o outro que está conectado ao ponto a. Calculando a série,
encontra-se Ceq = (800 / 6 ) µF. Por outro lado, note que
essa capacitância está em paralelo com o resistor de 6 kΩ. Portanto,
é fácil perceber que ao se calcular a tensão sobre o capacitor,
VC (t), é possível calcular i (t), simplesmente
dividindo-se essa tensão pelo valor do resistor, ou seja, 6 kΩ.
Seguindo esse raciocínio, a tensão sobre o capacitor com a chave S aberta
será a mesma tensão sobre o resistor de 6 kΩ. Para se calcular
essa tensão, pode-se empregar qualquer método estudado. Usando-se o método da
transformação de fontes, verifica-se que é possível reduzir a uma única fonte
de corrente de 1 mA apontando para cima. Os dois resistores de
2 kΩ e 3 kΩ, que após a transformação ficaram em paralelo,
resulta uma resistência equivalente de valor igual a 6/5 kΩ. Com isso,
através
de um divisor de corrente, é possível calcular i(0-)
que circula pelo resistor de 6 kΩ, ou seja:
Portanto, usando-se a lei de Ohm é possível calcular a tensão sobre
o resistor de 6 kΩ que é exatamente igual à tensão sobre o capacitor.
Logo:
Quando a chave S é fechada, o resistor de 2 kΩ é conectado em
paralelo com o capacitor e o resistor de 6 kΩ. Ora, como se sabe,
um capacitor não pode alterar bruscamente a tensão sobre seus terminais. Então, a
condição inicial é:
Agora é necessário calcular a tensão sobre o capacitor quando
t → ∞ (condição final). Do circuito, observa-se que o resistor
de 2 kΩ permanece em paralelo com o resistor de 6 kΩ.
Nesse caso, para se calcular a tensão sobre o capacitor basta substituir na
eq. 22-5.1 o valor de 6 kΩ
pelo paralelo dos dois resistores, ou seja, 1,5 kΩ. Note que não houve
mudança no valor da fonte de corrente. Então
De posse dessas informações, falta calcular o valor da constante de tempo do
circuito. Para tanto, anula-se as fontes de tensão e calcula-se a resistência
equivalente. Note que todos os resistores ficam conectados em paralelo.
Com isso, Req = 1,059 kΩ. Então, a constante de tempo τ do circuito é:
A eq. 22-03 permite escrever a tensão resultante sobre o capacitor, ou:
Como dito no início da solução do problema, para se calcular i (t) basta usar a relação abaixo:
Portanto, a equação solução para o problema é: