Problema 22-3    Fonte:   Problema 7.13 - página 367 -    THOMAS, Roland E. & ROSA, Albert J. & TOUSSAINT, Gregory J. - Livro: The Analysis & Design of Linear Circuits - Ed. John Wiley & Sons, Inc. - 6ª edição - 2009.

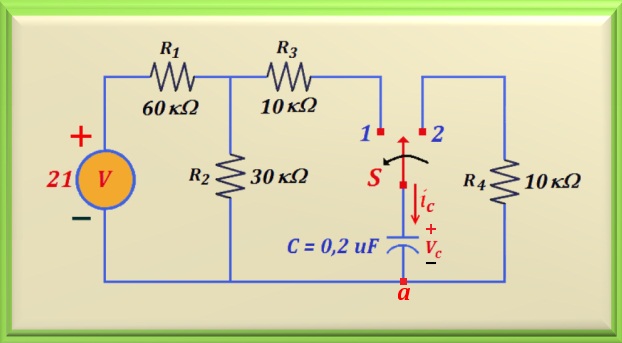
Na Figura 22-03.1, a chave esteve na posição 1 por um longo tempo. Em t = 0 a chave é passada para a posição 2. Determine v_C(t) para t ≥ 0

Solução do Problema 22.3

Como a chave esteve na posição 1 por um longo tempo, então a tensão inicial do capacitor é a tensão sobre o resistor que está em paralelo com ele. Como os tres resistores encontram-se em série e possuem os mesmos valores, então a tensão inicial do capacitor é V_i = 12 / 3 = 4 V. Ao passar a chave para a posição 2, devemos calcular o equivalente Thévenin desconsiderando o capacitor. Facilmente percebemos que este equivalente é formado pelo paralelo dos dois resistores, o que resulta uma resistência equivalente de 5 kΩ e uma tensão de Thévenin de 6 volts, pois os dois resistores têm valores iguais. Agora podemos calcular qual o valor da constante de tempo do circuito. Assim:

Conhecendo a constante de tempo do circuito, o valor inicial e final da tensão no capacitor, então vamos usar a eq. 22-03, mostrada abaixo, para se encontrar a expressão matemática que define a tensão entre os terminais do capacitor, ou seja:

Assim, temos:

Efetuando-se o cálculo, chegamos a:

Note que se tomarmos t = 0, encontraremos v_c = 4 volts (condição inicial), e se t → ∞ , encontraremos v_c = 6 volts (condição final).

De posse dessa equação, podemos agora calcular a tensão no capacitor para qualquer tempo desejado. Basta substituir o valor de t (em ms) na equação e efetuar os cálculos.