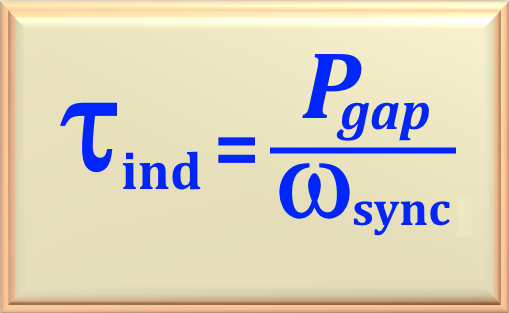Problem 108-4    Source:   Problem prepared by the site authors.

In a single-phase 6-pole motor with slip, s = 0.05, connected to a 60 Hz, 220 V network, it has an air gap power, P_gap = 800 W. It is also known that R_P = 27.4 Ω and R_R = 2.4 Ω. Determine:

a) the synchronous angular speed of the motor;

b) the electric current I₁ that flows through the motor;

c) the power in the air gap due to the forward field, P_Pgap, and the backward field, P_Rgap;

d) the torque induced in the motor rotor.

Solution of the Problem 108-4   

Item a

Since the motor has 6 poles and the network 60 Hz, then the synchronous angular velocity, ω_sync, using eq. 108-14 is:

Item b

To find the electric current I₁, we can use eq. 108-13. After some algebraic work, we obtain:

Item c

To find the air gap power due to the progressive field, we will use eq. 108-11.

And to find the air gap power due to the back field, we will use eq. 108-12.

Note that by subtracting these two values, we obtain the total power in the air gap, a value provided by the problem statement.

Item d

The torque induced in the machine, τ_ind, is given by eq. 107-32, repeated below.

Substituting the respective numerical values and performing the calculation, we obtain: