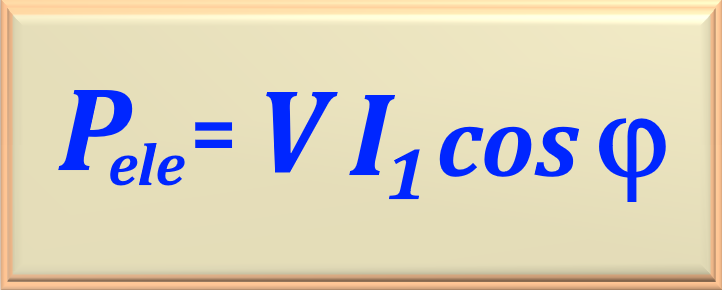Problem 108-10
Source: Problem prepared by the website authors.
The design of a split-phase, 127 V motor, with a nominal power of 1 HP, must have an efficiency of 68% and FP = 0.80.
Furthermore, it must have the following equivalent circuit parameters:
ZP = 8.0 + j 5.5 Ω ZR = 0.8 + j 0.7 Ω
The motor must operate at nominal voltage and frequency with the auxiliary winding open. It is known that core losses must be 40 W, rotational and supplementary losses 12.4 W. Determine:
a) the stator current;
b) the resistance value R1 of the main winding;
c) the reactance value X1 of the main winding.
Solution of the Problem 108-10
Since the motor's nominal power and efficiency are given, using eq. 108-31, it is possible
to calculate the motor's input power.
To calculate the electric current in the motor, we will use eq. 108- 29, shown below.
After some algebraic work, replacing the variables with their respective numerical values and performing the calculation, we obtain:
Since FP = 0.8, we can determine the lag angle of the current in relation to the voltage applied to the motor,
since arccos 0.8 = ± 36.87°. And, since the circuit is inductive,
that is, the power factor lags, we can write the phasor value of I1 as:
With the value of V = 127 V and I1 = 10.8° - 36.87° A, it is possible to calculate the total impedance of the motor,
simply by applying Ohm's law, that is:
It's important to understand that the value 9.4 Ω represents the value of the total resistance, Rtotal, of the
main winding. Since we know the value of RP = 8.0 Ω and RR = 0.8 Ω,
we can easily calculate the value of R1, since we know that:
Thus, making the numerical substitution in the variables and performing the calculation, we find:
To find the value of X1, we use the same line of reasoning as in the previous item. Thus, we have
Xtotal = 7.1 Ω and we know that:
By making the numerical substitution in the variables and performing the calculation, we obtain: