Problem 103-12    Source:  Problem prepared by the website author.

Suppose a DC motor that has a characteristic magnetization curve given by the following equation: E_A = - 0.000005 F² + 0.073 F + 5 . The field winding has 800 turns and for the speed of 1,500 rpm requires a field current of 5 A. In this case, the armature current is 100 A. Despise the armature reaction and take the armature resistance equal to 0.18 Ω. Find:

a) the induced voltage E_A in the machine and the supply voltage V_T of the engine.

b) if the field current is reduced to 4.5 A what is the new induced voltage and armature current?

c) the power developed by the machine in item a) and b).

Solution of the Problem 103-12   

Item a

To calculate the value of the induced voltage, first we must calculate the value of the MMF, F, which is given by eq. 102-03, repeated below. Remembering that we are neglecting the armature reaction.

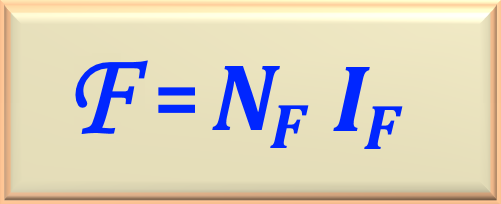
So, replacing the variables by their respective values, we get:

Now, using the equation given in the problem statement and the value of F,  we can calculate the value of induced voltage, or:

Doing the calculate, we find:

To find the motor supply voltage we will use the eq. 103-05, repeated below.

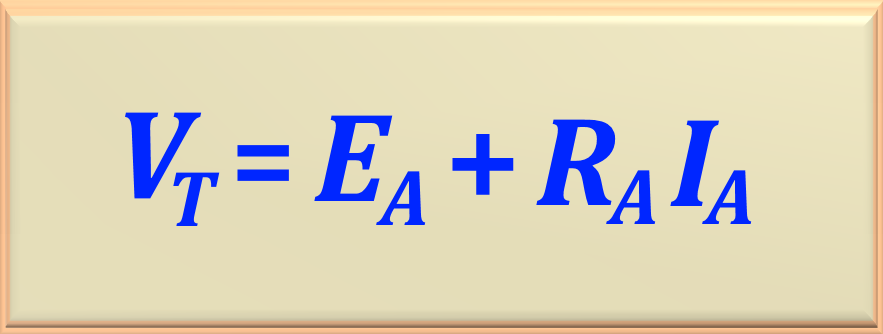
So, replacing the variables by their respective values, we get:

Item b

If the field current has been reduced to 4.5 A, then the new FMM, F, will be:

So the new value of E_A is:

Doing the calculate, we find:

And so, using the eq. 103-07 we can find the new value of I_A, or :

Item c

The power in the machine shaft is given by eq. 103-17, repeated below.

So in the case of item a), we have E_A = 217 V and I_A = 100 A. Soon:

And in the case of item b), we have E_A = 203 V and I_A = 177.8 A. Soon: