Problema 71-11
Fuente: Examen de Admision PUCRJ - RJ - 2009.
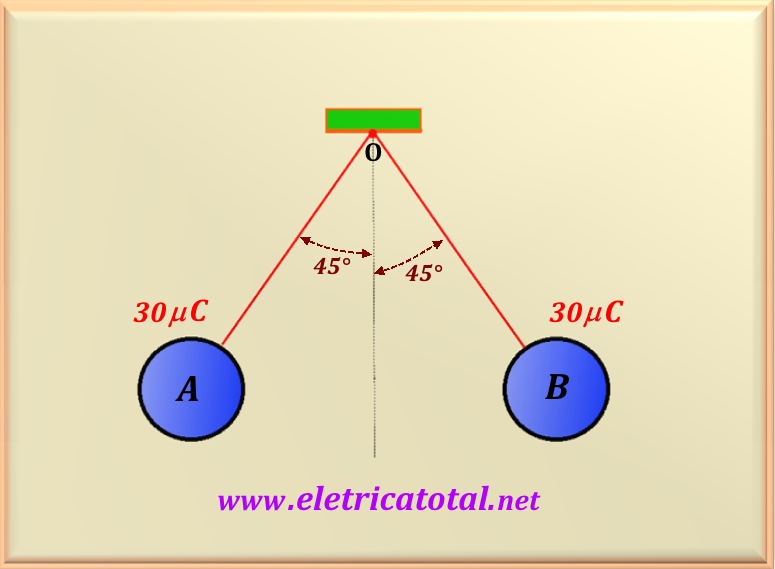
Dos esferas idénticas, cargadas con cargas Q = 30 µC, están suspendidas de
desde el mismo punto por dos alambres aislantes de la misma longitud que se muestra en
Figura 71-11.1.
En equilibrio, el ángulo formado por los dos alambres aislantes con la vertical es 45°.
Sabiendo que la masa de cada esfera es m = 1 Kg y considerando la constante de Coulomb
K = 9 x 109 N m2/C2, determinar la distancia entre los dos
esferas cuando están en equilibrio. Considerar g = 10 m/s2.
Solución del Problema 71-11
La Figura 71-11.2 muestra el esquema de las fuerzas que actúan sobre la esfera B y los
datos del problema sabemos que θ = 45°. Como las esferas tienen la misma polaridad
habrá una fuerza eléctrica repelente entre ellos. La tensión del alambre se puede descomponer
en dos componentes: uno en el eje x, como T senθ y otro en el eje y,
como T cosθ. Y en el eje y, apuntando hacia abajo, tenemos la fuerza de peso,
PB.
Sabiendo que m = 1 Kg, tenemos PB = m g = 10 N.
Dado que el sistema está en equilibrio, la suma algebraica de fuerzas en el eje y
debe ser igual a cero. Luego, la tensión en el alambre se puede calcular usando
Haciendo lo mismo para el eje y, encontramos
Ahora tenemos todos los datos necesarios para calcular la distancia entre las esferas.
Para ello usaremos la ley de Coulomb, según eq. 71-04.
Después de un arreglo algebraico en la ecuación, tenemos
Sustituyendo los valores numéricos y realizando el cálculo, encontramos
Entonces, extrayendo la raíz cuadrada, obtenemos