Problema 23-6    Fuente:   Problema 3.5 - página 11 -     Prof. Dr. João Costa Freire - Instituto Superior Técnico - Portugal     Libro: Análisis de circuitos - 2006. Disponible en: http://web.ist.utl.pt/pedro.m.s.oliveira/ProbAC.pdf

Determine la expresión para i_L en el circuito que se muestra en Figura 23-6.1.

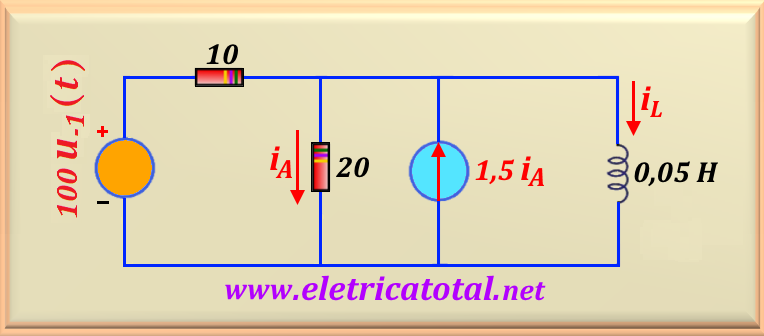
Solución del Problema 23-6

Tenga en cuenta que este problema utiliza una fuente independiente a través de una función salto o paso. De esta forma, sabemos que actuará solo después de t = 0. Antes de t = 0, su valor es nulo. Así, la fuente dependiente 1,5 i_A también será nula. Entonces, ya sabemos que

Para encontrar la corriente en el inductor durante el tiempo t → ∞, debemos calcular el Thévenin equivalente a la izquierda del inductor. Al quitar el inductor del circuito, nos queda el circuito que se muestra en Figura 23-6.2.

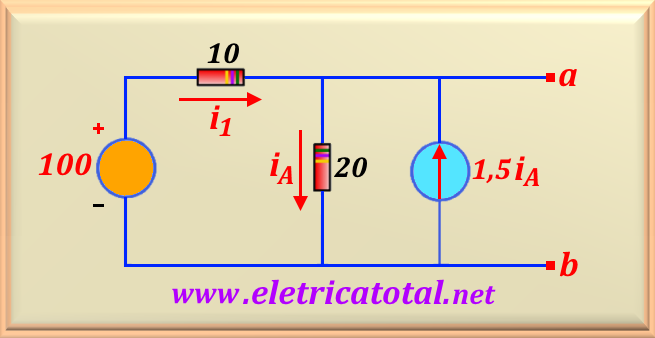
Necesitamos encontrar una relación entre i_A y i₁. Entonces, usando la ley de nodos para el nodo a, obtenemos:

Resolviendo esta relación, tenemos

Por otro lado, aplicando KVL al circuito formado por las dos resistencias y la fuente independiente, tenemos:

Reemplazando  ⓵  en  ⓶  y realizando el cálculo, obtenemos

Con el valor de i_A podemos calcular el valor de V_ab (voltaje de circuito abierto), que es el valor de V_th . Así

Para encontrar el valor de R_th , debemos cortocircuitar las terminales ab en el circuito Figura 23-6.2 y calcular la corriente de cortocircuito I_cc. Nos dimos cuenta de que al hacer el cortocircuito, la fuente dependiente y la resistencia 20 ohmios salen del circuito. De esta manera tenemos

Con estos datos y usando la eq. 15-01 podemos calcular el valor de R_th, o

En Figura 23-6.3 podemos ver el circuito equivalente de Thévenin.

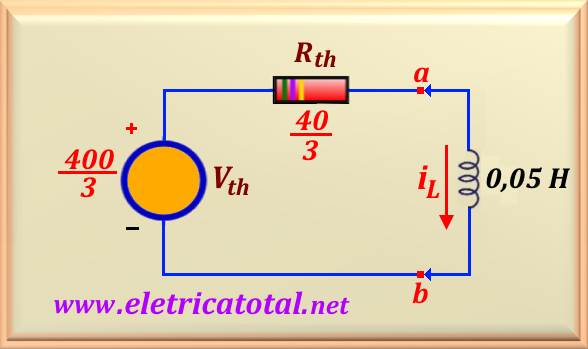
En este punto, podemos calcular la corriente en el inductor para el tiempo t → ∞, recordando que para este tiempo el inductor se comporta como un cortocircuito. Pronto:

Y ahora, basándonos en el circuito de la Figura 23-6.3, vamos a calcular la constante de tiempo del circuito, es decir

Con todos los datos calculados en la mano, podemos escribir la ecuación que expresa el comportamiento del circuito que se muestra en la Figura 23-6.1. Así