Problema 23-4 Fuente:
Ejercicio 7-15 - página 329 - THOMAS, Roland E. ,
ROSA, Albert J. , THOUSSAINT, Gregory J. - Libro: The Analysis & Design of Linear Circuits
- 6ª Edição - Ed. John Willey & Sons, Inc. - 2009.
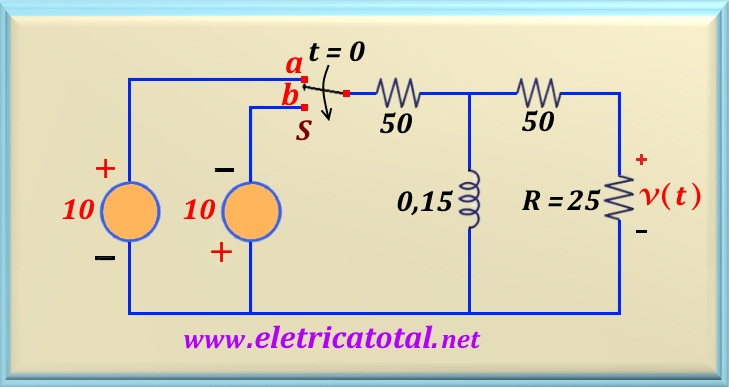
En el circuito de la Figura 23-04.1, el interruptor S ha estado cerrado durante mucho tiempo
en la posición a. En t = 0 el interruptor se ha movido a la posición b.
Calcular el voltaje v(t) para t > 0.
Solución del Problema 23-4
Como el interruptor S permaneció encendido durante mucho tiempo el inductor se comporta como un cortocircuito y la corriente i circula a través de la resistencia R en t = 0- entonces i (0-) = 0.
Luego, a través del inductor circula una corriente de:
Esta es la situación en t = 0-, cuando el interruptor S está en la posición a .
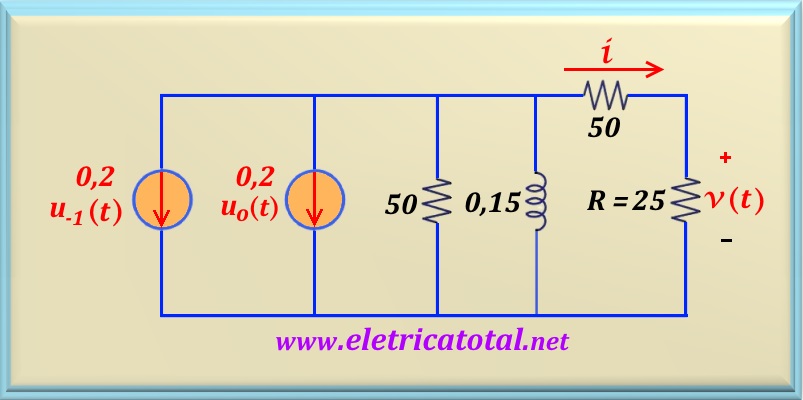
Pasar el interruptor a la posición b en t = 0 tiene la condición que se muestra en el circuito abajo. Observe que hicimos una transformación de fuente en el circuito que consiste en la fuente
10 voltios y la resistencia de 50 Ω. Encontramos una fuente de corriente de
0,2 u-1 (t) con la flecha apuntando hacia abajo. Y la resistencia de
50 Ω era paralela al inductor. Por otro lado, introdujimos una fuente impulsiva
de 0,2 A en lugar de la corriente que circula a través del inductor en
t = 0-. Vea la Figura 23-04.2.
Así, cuando en t = 0, si la fuente impulsiva actúa junto con la fuente escalonada, el inductor
se comportará como un circuito abierto. En esta situación, se puede calcular la corriente que fluye a través de la resistencia R, sabiendo que las dos fuentes que actúan juntas actúan como una sola fuente de corriente de 0.4 A .
Luego, usando un divisor de corriente, obtenemos:
Tenga en cuenta la señal negativa debido a la inversión de las fuentes de corriente. Ahora puedes calcular la voltaje en la resistencia R, es decir v(0), usando la ley de Ohm.
Es necesario calcular la corriente sobre la resistencia R cuando t → ∞.
Ahora, cuando t → ∞ el inductor se comportará como un cortocircuito y la fuente impulsiva no actuará.
Por lo tanto, se concluye que i(∞) = 0, porque la corriente de la fuente de corriente salto circulará completamente a través del inductor.
Para encontrar la solución al problema, necesitamos calcular la constante de tiempo del circuito. De
arriba del circuito, se observa que la resistencia de 50 Ω está en paralelo con los otros dos que están en serie Por lo tanto, al realizar el cálculo, se encuentra la resistencia equivalente de
30 Ω . Entonces
Para encontrar la solución del problema solo use la eq. 23-03. Luego: