Problema 22-3    Fuente:   Problema 7.13 - página 367 -    THOMAS, Roland E. & ROSA, Albert J. & TOUSSAINT, Gregory J. - Libro: The Analysis & Design of Linear Circuits - Ed. John Wiley & Sons, Inc. - 6ª edição - 2009.

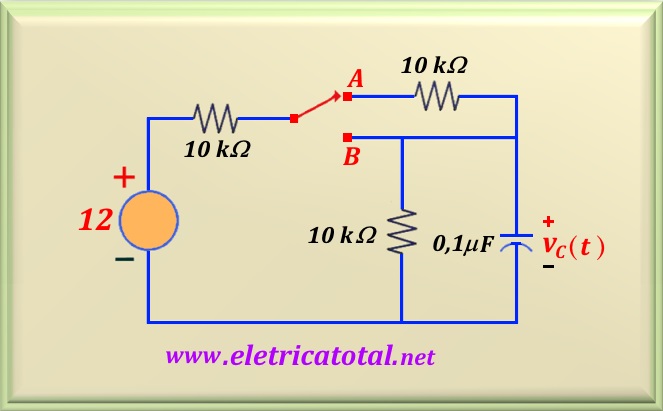
En la Figura 22-3.1, la clave ha estado en la posición A durante mucho tiempo. Ent = 0 la llave se pasa a la posiciónB. Determine v_C(t) para t ≥ 0

Solución del Problema 22.3

Como el interruptor ha estado en la posición A durante mucho tiempo, el voltaje inicial del condensador es el voltaje en el resistor que es paralelo a él. Dado que las tres resistencias están en serie y tienen los mismos valores, por lo que el voltaje inicial del condensador es V_i = 12 / 3 = 4 V. Al pasar la llave a la posición B , debemos calcular el equivalente Thévenin sin tener en cuenta el condensador. Nos damos cuenta fácilmente de que este equivalente está formado por el paralelo de las dos resistencias, lo que resulta en una resistencia equivalente de 5 kΩ y un voltaje Thévenin de 6 voltios, ya que ambas resistencias tienen valores iguales. Ahora podemos calcular cuál es la constante de tiempo del circuito. Así:

Conociendo la constante de tiempo del circuito, el valor inicial y final del voltaje del condensador, entonces usemos eq. 22-03 , que se muestra a continuación, para encontrar la expresión matemática que define el voltaje entre terminales de condensador, a saber:

Así, tenemos:

Realizando el cálculo, llegamos a:

Tenga en cuenta que si tomamos t = 0, encontraremos  v_c = 4 voltios   (condición inicial), y si t → ∞ , encontraremos v_c = 6 volts (condición final).

Con esta ecuación, ahora podemos calcular el voltaje del condensador para cualquier momento deseado. Simplemente reemplace el valor de t (en ms ) en la ecuación y realice los cálculos.