Problema 24-1    Fonte:   Exemplo 8.1 - página 177 - NILSSON, James W. & RIEDEL, Susan A. - Livro: Circuitos Elétricos - Editora LTC - 5ª edição - 1999.

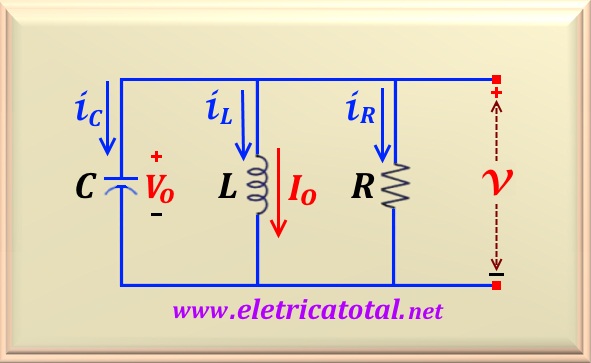
No circuito mostrado na Figura 24-01.1, temos que R = 200 Ω, L = 50 mH e C = 0,2 µF. Determine:

a) as raízes da equação característica que descreve o comportamento transiente do circuito.

b) a resposta do circuito é superamortecida, subamortecida ou criticamente amortecida?

c) repita os itens (a) e (b) para R = 312,5 Ω.

d) qual deve ser o valor de R para que a resposta seja criticamente amortecida?

Solução do Problema 24-1

Item a

Inicialmente, deve-se calcular os valores de α e ω_o, pois se conhece os valores de R, L e C. Assim:

E para o valor de ω_o:

Com esses dados podemos escrever as raízes da equação característica usando a eq. 24-06 e eq. 24-07. Assim:

Efetuando-se o cálculo:

Para se encontrar a outra raiz, deve-se usar a eq. 24-07. Após a substituição numérica e efetuando-se o cálculo, obtém-se:

Item b

Com os valores calculados no item a, verificamos que α > ω_o e portanto a resposta do circuito é superamortecida.

Item c

Alterando o valor de R para 312,5 Ω, obtém-se um novo valor para α, porém o valor de ω_o continua sendo o mesmo, pois seu valor não depende de R. O novo valor de α é:

Como α < ω_o, então o circuito tem uma resposta subamortecida. Para este tipo de resposta, sabe-se que as raízes da equação característica são complexas. Então, substituindo pelos valores numéricos e após efetuar o cálculo, obtém-se:

Item d

Para se conseguir uma resposta criticamente amortecida, sabe-se que α = ω_o. Neste caso, α = ω_o = 8.000 rad/s. Então o valor de R será:

Fazendo a substituição numérica e efetuando-se o cálculo: