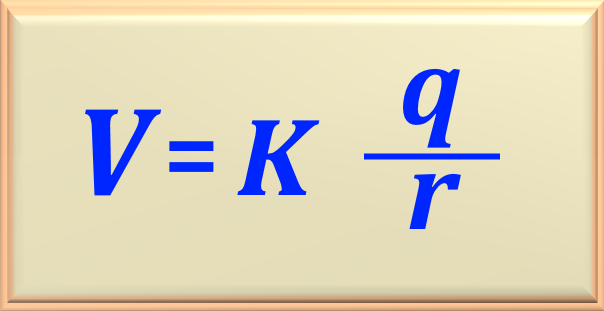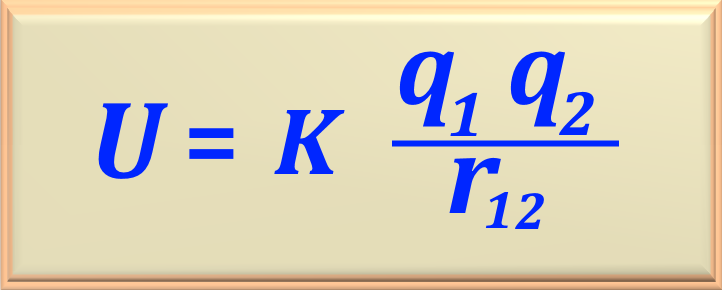Problema 72-1    Fonte:  Exemplo 23-2 - TIPLER, Paul - MOSCA, Gene -    Livro: Física - Vol. 2 - 5ª Edição - Ed. LTC - 2006.

a) Calcule o potencial elétrico a uma distância r = 0,529 x 10^-10 m de um próton (Esta é a distância média entre um próton e um elétron no átomo de hidrogênio).

b) Qual é a energia potencial elétrica do elétron e do próton a essa distância de separação?

Solução do Problema 72-1   

Item a   

O potencial devido ao próton pode ser calculado usando a eq. 72-09, reproduzida abaixo.

Então, substituindo pelos valores numéricos, encontramos:

Efetuando o cálculo encontramos o valor do potencial elétrico, ou

Item b   

Para calcularmos a energia potencial entre as duas partículas podemos usar a eq. 72-11, reproduzida abaixo.

Então, substituindo pelos valores numéricos, encontramos:

Efetuando o cálculo encontramos o valor da energia potencial, ou

Dividindo o valor encontrado pela carga da partícula, obtemos o valor da energia em eV , ou seja, U= 27,20 eV. Note que usando a eq. 72-07, já que conhecemos ΔV, vamos obter o mesmo resultado. Confira !!!!

Observação: Se o elétron estivesse em repouso, a essa distância do próton, seriam necessários, no mínimo, 27,2 eV para removê-lo do átomo. Entretanto, como o elétron gira em torno do próton, ele possui uma energia cinética igual a 13,6 eV. Então, a energia total que o elétron possui no átomo é de 13,6 - 27,2 = -13,6 eV. Logo, a energia mínima necessária para remover o elétron do átomo é de 13,6 eV. Essa energia é conhecida como energia de ionização.