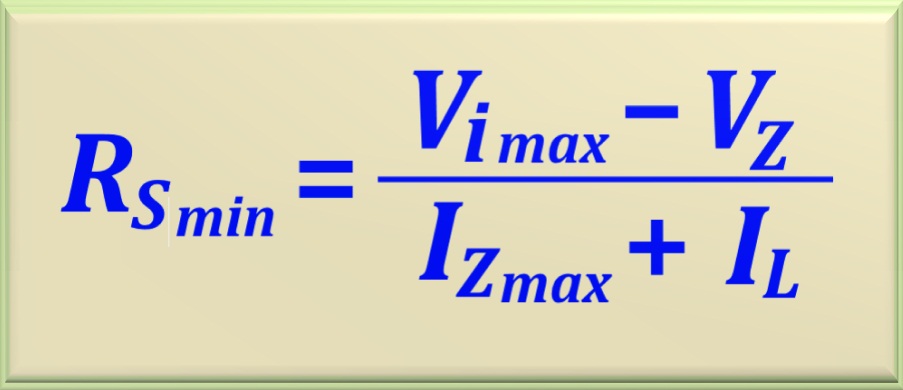Problem 64-3    Source:   Problem elaborated by the author of the site.

Be the circuit shown in the Figure 64-03.1. Assume that Vi = 27 volts with ΔV = 4 volts and V_Z = 15 volts. The current consumed by the load is 100 mA. Determine the values of R_Smax , R_Smin and what the power in the zener.

Solution of the Problem 64-3   

Note that the input voltage is variable but the load is constant. Then there will be variation in the current flowing through the zener. Therefore, the case 3 is studied in the Zener Diode Circuit Design item (Here!!). Since the model of the zener to be used was not provided, we must start by stipulating a maximum current for the zener. Since the load consumes 100 mA, we can make the maximum current for the zener of, say, I_Zmax = 200 mA. In this case, the power in the zener will be:

Commercially there is no zener for this power. The closest is 5 watts. So let's assume that the zener is 5 watts. We can calculate the maximum current that zener can support, or:

Then, I_Zmin will be:

With these two values we will calculate R_Smin and R_Smax using the two equations studied. Let's repeat them here.

Recalling that in this problem, V_i(min) = V_i - (ΔV/2) = 27 - 2 = 25 volts and to find the maximum, V_i(max) = V_i + (ΔV/2) = 27 + 2 = 29 volts. Then:

And in turn

Note that R_Smax > R_Smin enabling the project. We can choose to the series resistor the average value of the calculated values. So, R_S = 54 ohms. A commercial value that can be used is R_S = 56 ohms

Note that the current through R_S is not constant. Depends on variations in input voltage. So we have I_Smax = (V_i(max) - V_Z) / R_S = 0.25 A . In this way, the maximum current flowing through the zener is I_Zmax = (I_Smax - I_L) = 0.15 A . Therefore, zener supports this current without problems. The power dissipated by it will be:

Using a 5 watt zener will not have any problems with the design.