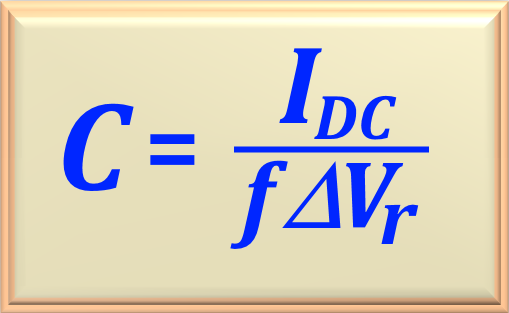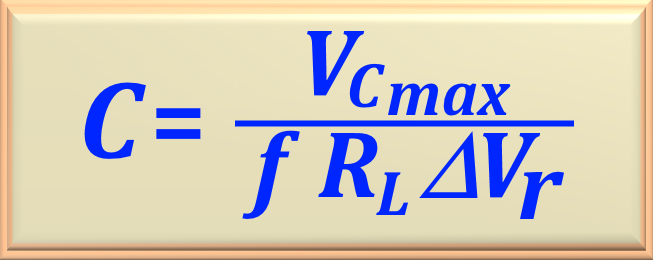Problem 62-2
Source: Problem elaborated by the author of the site.
In the secondary of a transformer the voltage is Vs = 15 Vrms.
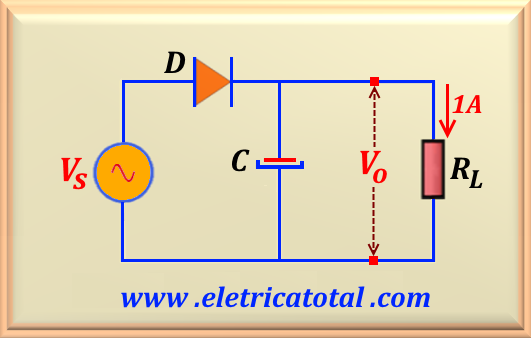
Using a half-wave rectifier, calculate the capacitor value for a 4% ripple and the load value
if it consumes a current of 1 A (Consider f = 60 Hz). Make a comparison between the values
found using the approximation VCmax ≅ VDC and without using the approximation.
Solution of the Problem 62-2
Since the secondary voltage has been supplied in rms values, we must transform to peak voltage,
that is, Vp = √2 x 15 = 21.21 V. The circuit to be considered in the calculations
is that shown in Figure 62-02.1. Note that diode D is in series with the secondary of the transformer,
which is represented in the figure by the voltage source, Vs. Therefore, to know the maximum voltage
across the capacitor, we must subtract from the peak voltage the value of the voltage drop across the diode. So the
maximum voltage across the capacitor will be
VCmax = 21.21 - 0.7 = 20.51 V.
As a setting of 4% is desired, this results in
ΔVr = 0.04 x 20.51 = 0.82 V.
To calculate the value of C, without approximation, we will use the eq. 62-08 reproduced below.
So, substituting the numerical values, we get
As stated in the theoretical part, the value found with the approximation has an error less than 3% when compared with the value found without the approximation. Also, we should note that the default value of a capacitor on the market does not take into account this difference. Therefore, it is possible to use the approximation without loss of precision.