Problem 62-1    Source:  Problem elaborated by the author of the site.

In the secondary of a transformer the voltage is V_s = 10.7 sin t. Using a half-wave rectifier, calculate the mean value of the waveform at the rectifier output.

Solution of the Problem 62-1   

As we saw in the previous problem, we must subtract the voltage drop on the rectifier diode from the input voltage peak value ( V_peak = 10.7  V ) to get the correct voltage value at the rectifier output. Then, after rectification, the value of the maximum output voltage is V_max = V_peak - 0.7 = 10 volts. The Figure 62-01.1 shows the waveform that appears on the rectifier output.

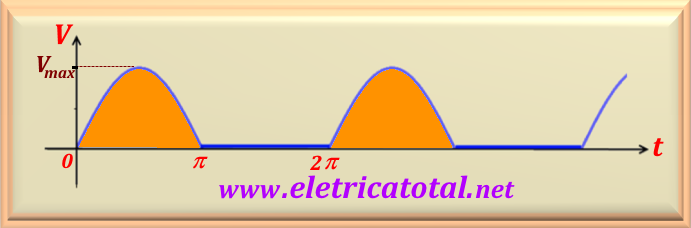
To solve this problem we will use the basic principles of integration of trigonometric functions. Based on this figure, we can make some considerations about calculating the Mean value of a half-wave rectified wave.

Let the input voltage be given by V = (V_max + 0.7) sin t . After half wave rectification, the maximum voltage at the rectifier output is given by V_max, as shown in Figure 62-01.1 . The average value of a function is given by:

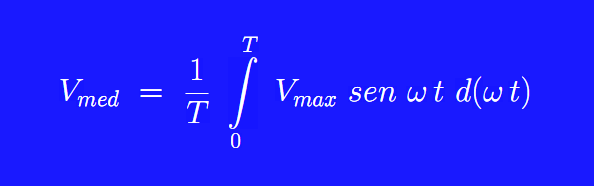
From Figure 62-01.1, we clearly see that T = 2 π. The integration ranges are two: the first, with the value of the function, has the limits 0 and π: the second, has the limits π and 2 π and the value of the function in this range is zero. Soon:

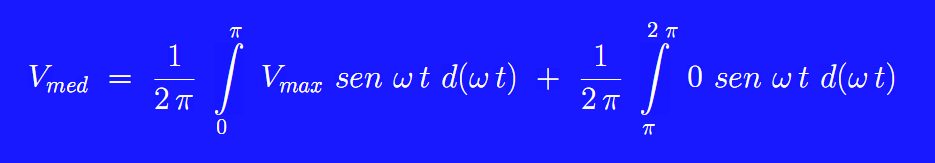
Doing the calculation we get:

Thus, the mean value of the function is given by:

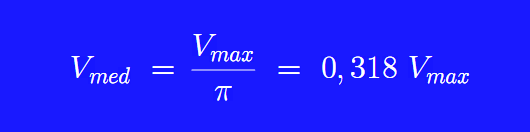
So, as we know that V_max = 10 volts, the result of the problem is: