Problem 10-22 Source:
Problem elaborated by the author of the site.
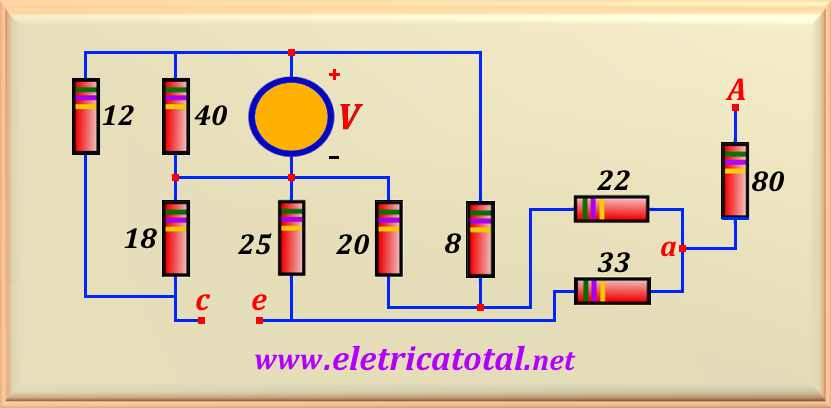
From the circuit shown in Figure 10-22.1, knowing that V = 60 volts, determine:
a) The voltage in the point A, that is, VA.
b) The potential difference between the points c-e.
Problem solving using: Kirchhoff's Law
click here!
Solution of the Problem 10-22 -
Ohm's Law
First, we must point out that to calculate the voltage value at point A,
it turns out
that nothing is connected to this point. This way, by the resistor of 80 ohms,
no current
will circulate and it can be removed from the circuit,
because the voltage at point A is the same as point a . On the other
hand, the
40 ohm resistor is connected in parallel with the voltage source. So, it can
also be removed
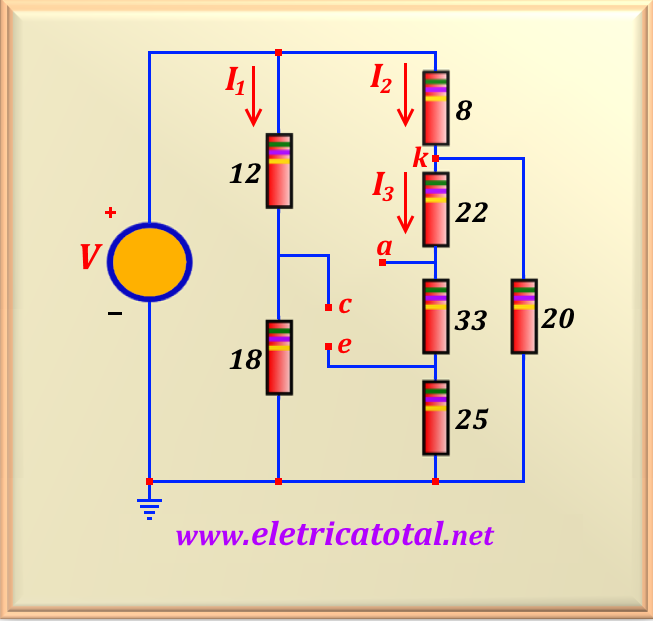
from the circuit without prejudice to its solution. So, in Figure 10-22.2
we show
the same circuit, but with a new topology without the two resistors mentioned above,
for a better understanding of the solution.
Let's start by calculating the currents I1, I2 and I3.
We easily calculate I1 using the law of Ohm , that is
For the calculation of I2 it is necessary to find the equivalent resistance
value between the point k and the ground. It is noticed that passing through the points
a and e, we have three resistances in series, resulting in a single one of value
80 Ω. And this is in parallel with that of 20 Ω, resulting a
equivalent resistance of 16 Ω. Adding this value to that of 8 Ω,
we get a total of 24 Ω. So the value of I2 , using the law of Ohm , is
And to find the value of I3 just apply a current divider, or
To calculate the potential difference between points c-e , we must calculate
the voltage at point c and at point e . So:
And by definition, we know that Vce = Vc - Ve. Then