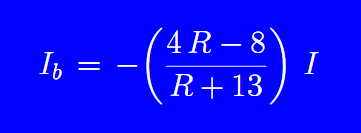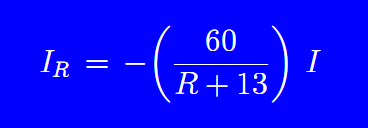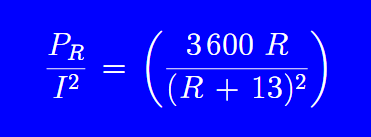Problem 15-13    Source:    Problem elaborated by the author of the site.

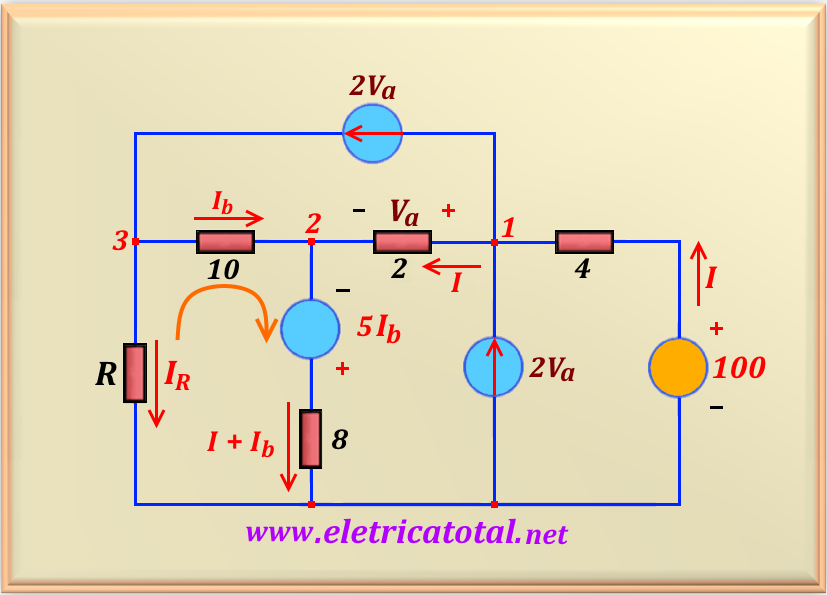
Based on the previous problem, considering the circuit shown in Figure 15-13.1, determine to which value of R the maximum power dissipation occurs in it.

Solution of the Problem 15-13

Note that we already determined in the previous problem that I = I_a. Therefore, we will solve using as variable the current I. Thus, we conclude that V_a = 2 I, and that the current source 2 V_a = 4 I. So we can write that I_R = 4 I - I_b. After these considerations and based on the circuit shown in Figure 15-13.1, let's make the mesh indicated by the orange arrow. So:

Algebraically rearranging the above equation, we will find a relation between I and I_b. So:

As I_R = 4 I - I_b, replacing I_b with the above equation and effecting an algebraic manipulation we will find:

Knowing the value of I_R , we can calculate the power dissipated by R and then calculate the value of R for get the maximum power dissipated by it. This requires some basic knowledge of Advanced Calculation . For those who know this content we have prepared an article in PDF that can be accessed   Click HERE!!!.  But we can advance that the value found is:

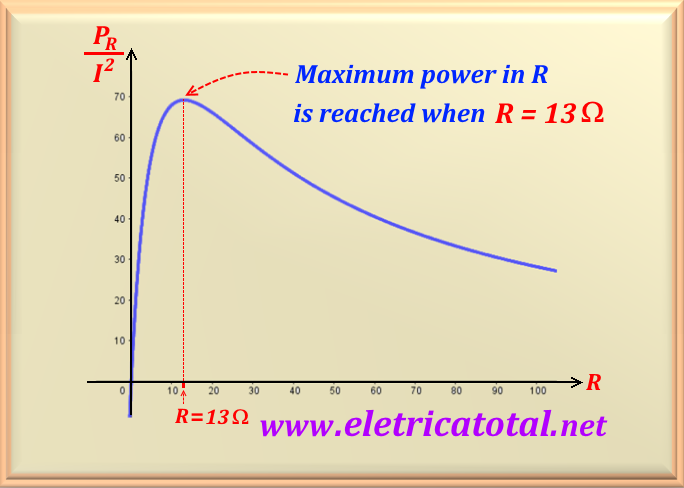
To confirm this result we show in the figure below a graph, which was obtained from the power equation dissipated by the resistance R given by the expression below:

Making an algebraic arrangement, we get:

So by plotting this equation in a program like Geogebra, we get the curve shown in the Figure 15-13.2. Note that the graph clearly shows that the maximum power dissipated by R is when its value is equal to R = 13 ohms.