Problem 11-2    Source:    Problem 4.12 - page 96 -    NILSSON & RIEDEL -    Book: Circuitos Elétricos - 8ª edição - Ed. Pearson Education do Brasil - 2010.

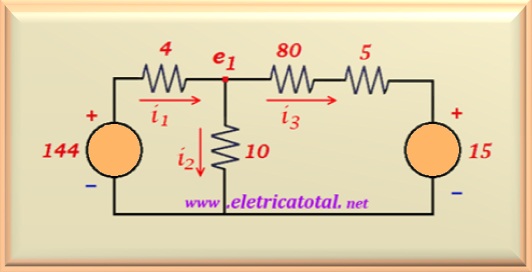
In the circuit show in Figure 11-02.1, calculate:

The voltages in the nodes and the currents i₁ , i₂ , i₃ and i₄.

Solution of the problem using Node Voltage Method   click here!

Solution of the problem using Superposition Method   click here!

Solution of the problem using Thévenin/Norton Method   click here!

Solution of the Problem 11-2 -  Method of Transforming Sources

We know that by the method of transforming sources any current source that is in parallel with one or more resistors can be replaced by a voltage source in series with a resistor whose value is the equivalent resistance of the resistor (s) that is found in parallel with the current source. Always remember that the value of the voltage source is the product between the value of the current source and the value of the resistor in parallel. Then, applying this principle on the right side of the circuit you can see the result in the Figure 11-02.2.

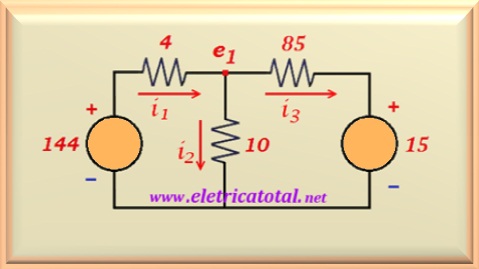
Now we can add the two resistors that are in series and we obtain the circuit show in Figure 11-02.3:

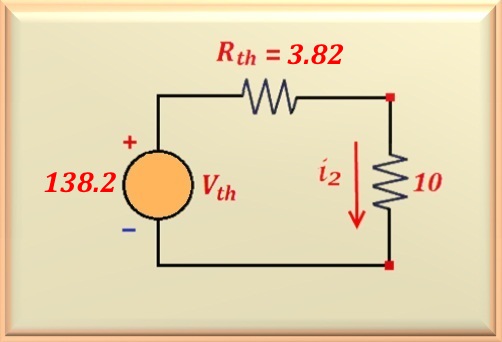
Note that after the source transformation that was performed, we obtained the same circuit of Problem 11-1    click here!. And this circuit we already know how to solve. So by making more source transformations we can go straight to the result. The circuit of the Figure 11-02.4 is reached.

So to calculate i₂ just apply the law of Ohm and find the searched value.

With the value of the i₂ and looking at the original circuit, we easily calculate the values of the other variables, as can be seen below.

With the value of the e₁ you can calculate the currents i₁ and i₃. So let's calculate yours values:

The current i₄ is the sum of i₃ with a current source of 3 A and e₂ is the product of i₄ and the resistor of 5 ohms. So:

Therefore, as our results satisfy the equations of mesh and the equations of nodes we can now perform a power balance of the circuit. So we will prove that these results are correct.