Problem 11-1    Source:   Problem elaborated by the author of the site.

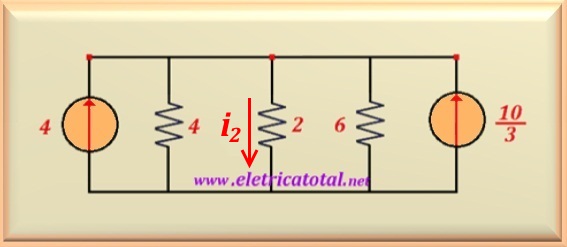
In the circuit show in Figure 11-01.1, calculate:

a) The currents i₁ , i₂ and i₃.

b) The voltage of the node e₁.

Solution of the problem using Kirchhoff Method   click here!

Solution of the problem using Superposition Method   click here!

Solution of the problem using Thévenin/Norton Method   click here!

Solution of the problem 11-1 - Method of Transforming Sources

We know that by the method of transforming sources any voltage source that is in series with one or more resistors can be replaced by a current source in parallel with a resistor whose value is the sum of the value (s) of the resistor (s) found in series with the voltage source. We recall that the value of the current source is the quotient between the value of the voltage source and the value of the resistor (or equivalent resistance) that is in series with the voltage source.

Thus, realizing that we have two voltage sources in series with resistors we apply the principle of transforming fonts. In the Figure 11-01.2 we redesign the circuit with the applied transformation.

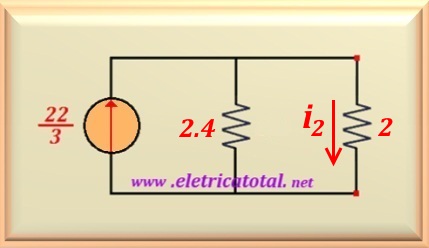
As the two sources of current point in the same direction, then we can sum them together. The 4 and 6 ohms resistors are in parallel and we can replace them with a single value equal to 2.4 ohms as shown in the circuit in the Figure 11-01.3.

Now just apply a current divider and we can compute i₂, that is:

With the value of i₂ and looking at the original circuit we easily calculate the values of the other variables as can be seen below.

With the value of e₁ we can calculate the currents i₁ and i₃. So let's calculate your values.

As we see the current i₃ is negative meaning that its direction is contrary to that established in the original circuit. To verify if the results found are correct we can make a power balance, as shown below.