Problema + Difícil 52-3    Fuente:   Adaptado del Problema 3 del 1er Examen de 2019 - Disciplina Circuitos Eléctricos de Facultad de Ingeniería - PUCRS - 2019.

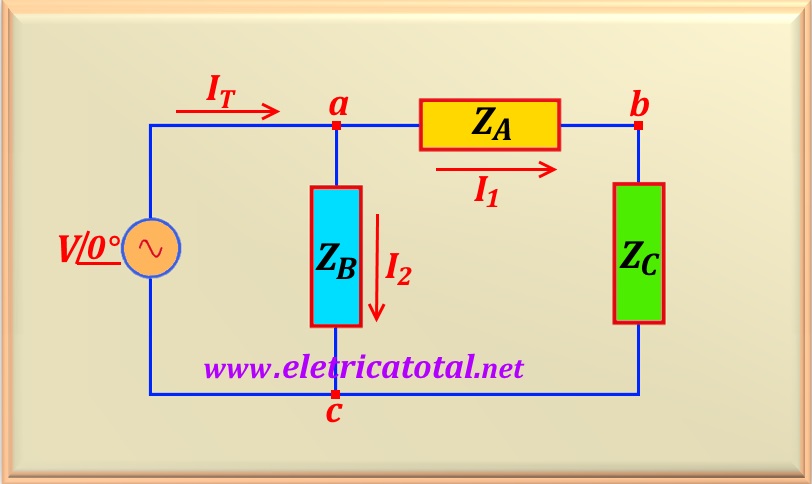
Para el circuito que se muestra en la Figura 52-03.1, se sabe que:

Dicho esto, recordando el principio de conservación de la potencia compleja, calcula:

a) El factor de potencia total de las cargas.

b) La corriente efectiva consumida por las cargas.

c) ¿Qué potencia reactiva debe generar una batería de condensadores conectada en paralelo para que el factor de potencia del Circuito unidad.

d) Piña, un ingeniero cauteloso diseñó este banco de condensadores con el doble de la potencia reactiva calculada en el ítem anterior. Explique las consecuencias de este error.

Solución del Problema + Difícil 52-3

Consideraciones Iniciales

En base a esta última información, como R_C = X_C, entonces P_C = Q< sub >C. Por lo tanto, la potencia de carga compleja C se puede escribir como:

Por otro lado, la carga A es resistiva y consume 100 W. Por lo tanto, se puede escribir la potencia compleja consumida por el cargas A y C, o:

Para calcular S_B, debe calcular I₂. Así:

Realización del cálculo:

Con este dato se puede calcular S_B, recordando que para calcular esta potencia es necesario utilizar el complejo actual I₂, o:

Ahora es posible calcular la potencia compleja total consumida por el circuito. Entonces:

Item a

A partir del valor del ángulo de S_T se obtiene el factor de potencia del circuito, o sea:

Item b

Para calcular el valor de I_T, utilice el hecho de que S_T = V I^* T. Entonces:

Realización del cálculo:

Entonces el valor de I_T es:

Item c

Para que el factor de potencia sea unitario, la potencia reactiva debe ser nula. Como ya se calculó,S_T = 400 + j 300. Entonces la potencia de los capacitores debe anular la porción j 300 de S_T, es decir:

Item d

Como el ingeniero Ananás calculó el doble de la potencia requerida, es decir, Q_C = - 600   VAr, entonces el factor de potencia va de 0,800 inductivo a 0,800 capacitivo.