Problema + Difícil 10-1 Fuente:
Problema elaborado por el autor del sitio.
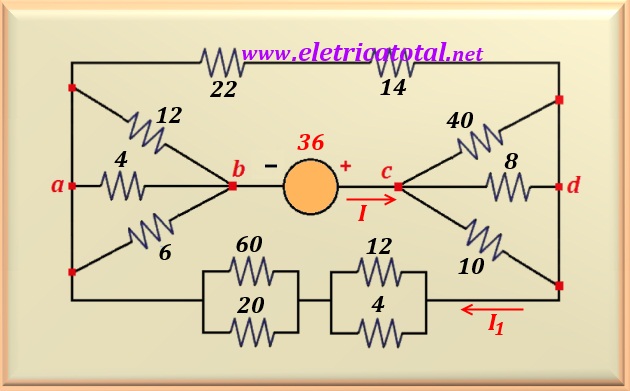
Determina el valor de I1 y I en el circuito que se muestra en la Figura 10-01.1.
Solución del Problema + Difícil 10-1
Tenga en cuenta que las tres resistencias que son
entre los nodos a-b, están en paralelo. Lo mismo sucede con los tres
resistencias que se encuentran entre los nodos c-d. Calculando el paralelo de estas resistencias,
da como resultado una resistencia equivalente de 2 Ω para aquellos entre los nodos a-b y 4 Ω para aquellos que
están entre los nodos c-d. En la parte superior del circuito, interconectando los nodos a-d,
hay dos resistencias en serie. Realizando el cálculo, resulta una resistencia
equivalente a 22 + 14 = 36 Ω. En la parte inferior del circuito,
también interconectando los nodos a-d, hay dos conjuntos
resistencias que están en paralelo. Resolviendo este paralelo, da como resultado 15 Ω
para el conjunto izquierdo y 3 Ω para el conjunto derecho.
En la Figura 10-01.2, el circuito reducido se muestra después de los cálculos de las distintas asociaciones.
Tenga en cuenta que la corriente I1 continúa fluyendo a través de las resistencias inferiores
del circuito.
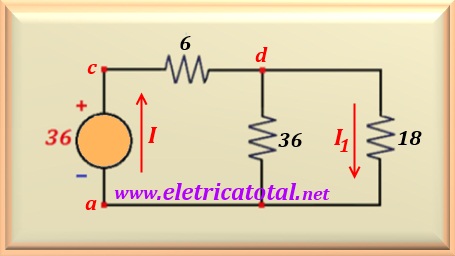
En la Figura 10-01.3, la topología del circuito ha cambiado un poco, mostrando que la
resistencia de 6 Ω que está entre los nodos c-d, es el resultado de
asociación en serie de las dos resistencias que estaban en serie con la fuente de tensión.
Las resistencias que interconectaban los nodos a-d se colocaron en paralelo.
Y por la resistencia de 18 Ω, circula I1. Para calcular el valor de I, primero debes calcular el paralelo de las
resistencias 18 Ω y 36 Ω. Realizando el cálculo, el resultado es el valor
de 12 Ω. Sumando a la resistencia de 6 Ω (ya que están en serie)
encuentre la resistencia equivalente de todo el circuito, es decir:
A partir de este momento se puede calcular el valor de I. Así:
Para calcular I1, se aplica un divisor de corriente.
Donde 12 Ω es el valor del paralelo entre las resistencias 18 Ω y 36 Ω.
Intentamos calcular la corriente eléctrica en la resistencia de 18 Ω, entonces: