Problem 15-9    Source:    Problem elaborated by the author of the site.

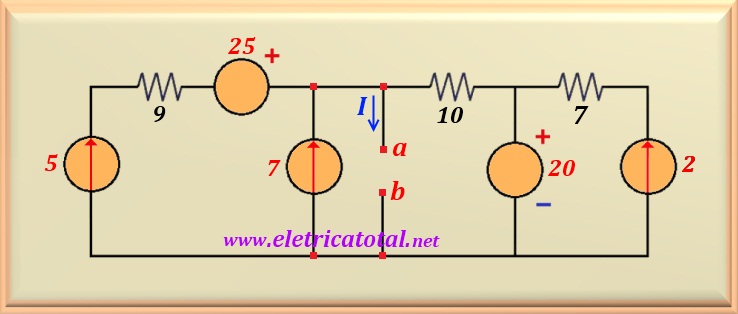
Determine the value of I that circulates between the points a and b in the circuit shown in Figure 15-09.1, when between these points are inserted resistors of values equal to 4, 10 and 25 ohms. In addition, calculate the power dissipated in each resistor.

Solution of the Problem 15-9   -    Thévenin/Norton Method

Through the circuit we realize that the current source of 5 A is in series with the resistor of 9 ohms and the voltage source of 25 volts. Therefore, we can eliminate these last two components, since they are in series with the current source. And as we know, in this case, the source of current predominates. In this way, we have the two current sources in parallel. On the other hand, the 7 ohm resistor and the current source of 2 A that is in series with it can also be eliminated from the circuit because they are in parallel with the voltage source of 20 volts. 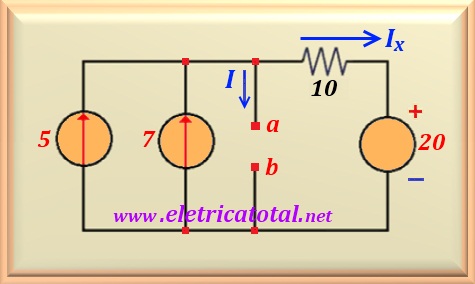So, we stayed with the simplified circuit shown in the Figure 15-09.2.

From the circuit shown in the figure above, I = 0. Then I_x = 7 + 5 = 12 A. With this data, we easily calculate the open circuit voltage at points a-b, which represents the Thévenin Voltage for this circuit.

And to determine R_th, is enough eliminate the current sources and short-circuit the voltage source. Thus, the only resistor of the circuit remains, therefore:

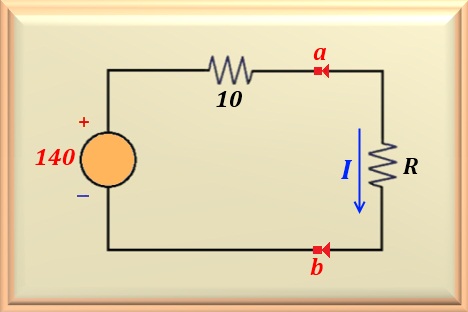
In the Figure 15-09.3, we can appreciate the Thévenin equivalent of the circuit. Note that among the points a-b was put the resistor R that will assume the values of the statement of the problem.

To R = 4 ohms

When R = 4 ohms the current I that will circulate through the circuit will be:

And the power dissipated by this resistor will be:

To R = 10 ohms

When R = 10 ohms the current I that will circulate through the circuit will be:

And the power dissipated by this resistor will be:

To R = 25 ohms

When R = 25 ohms the current I that will circulate through the circuit will be:

And the power dissipated by this resistor will be:

Note that the result of this problem is in perfect agreement with the theorem of Maximum Power Transfer.