Problem 13-8    Source:   Problem developed by the site author.

For the circuit shown in Figure 13-08.1, knowing that V = 60 volts and using Kirchhoff's law, determine:

a) The values of I and I₁.

b) The power dissipated by the resistor 14 ohms.

Solution of the using Ohm's Law   click here!

Solution of the Problem 13-8   -    Método Kirchhoff

Item a

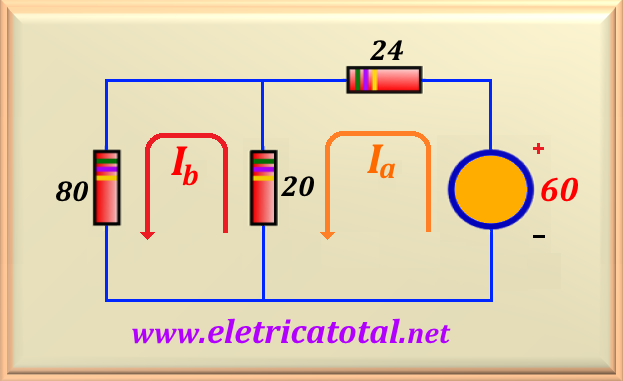
Using the current mesh method ( Kirchhoff's Law ) we know that in a closed loop, the algebraic sum of the voltages must be equal to ZERO . In Figure 13-08.2 we see the redesigned circuit where we show the sense (counterclockwise) of the currents I_a and I_b. In addition, we aggregate the values of the resistors of each branch.

We can write the two equations for the two loops in the circuit, obeying the counterclockwise direction of the currents. See, below, the system of equations that will allow you to solve the circuit.

So we have a system of two equations with two unknowns, which can be solved by Crammer rule, by substitution, etc ... After the calculations we find the values of I_a and I_b.

Now, comparing the two circuits, it is possible to notice that I = I_a and that I₁ = I_a - I_b. So, we get:

Item b

To calculate the power dissipated by the resistor of 14 Ω, we must pay attention that the current that flows through it is I . Therefore, using the equation eq. 7-02 studied in chapter 7 , we have