Problem 10.12 Source:
Problem 2.57 - page 74 - IRWIN, J. David - Book:
Análise de Circuitos em Engenharia - 4ª edição - Ed. Pearson Education do Brasil - 2013.
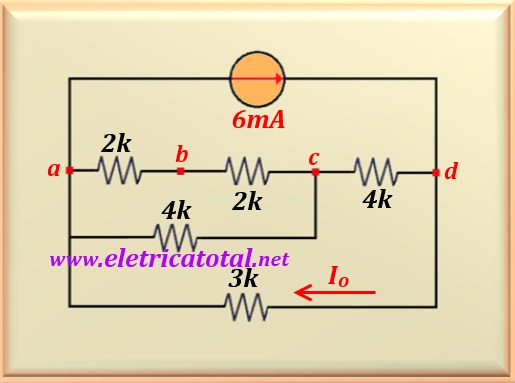
Determine the value of Io in the circuit show in
Figure 10-12.1.
Solution of the problem 10-12
To begin solving this problem the nodes will be given names. In this way, it is
there are two resistors in parallel between nodes a-b. One of 6 kΩ
and another of 3 kΩ. Solving this parallel is an equivalent resistance
of value equal to 2 kΩ . Between the c-d nodes the same
thing happens. There are two resistors in parallel: one of 6 kΩ and
another of 12 kΩ. Solving this parallel is
finds an equivalent resistance of value equal to 4 kΩ. Thus, one can
simplify the circuit as shown in the Figure 10-12.2.
Note that in the branch a-b-c there are two series resistors of
2 kΩ each. Therefore, adding the two we have a single resistor
of 4 kΩ.
However, this resistor is in parallel with the other one of 4 kΩ.
Now, by calculating the parallel, it resolves a single resistor of
2 kΩ that interconnects the nodes a-c .
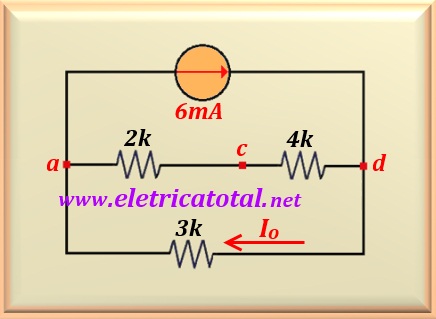
Thus, the circuit has been reduced significantly, conform Figure 10-12.3 . Finding the value of the
series of 2 kΩ and 4 kΩ , we can calculate the value
of Io ( which results in a 6 kΩ resistor).
The parallel of the resistors of 6 kΩ and 3 kΩ must be
calculated. This originates a single resistor of 2 kΩ between nodes
a-d . Then, the potential difference between nodes d-a will be:
Now, to find the value of Io, just apply the Ohm's law :
Another way to find the value of I o, without needing to
compute Vda, would apply a current divider. Like this: