Problema 85-3    Fonte:  Adaptado do Exercício 22.8 - página 677 - BOYLESTAD, Robert L. - Livro: Introdução à Análise de Circuitos - 10ª Edição - Ed. Prentice Hall - 2008.

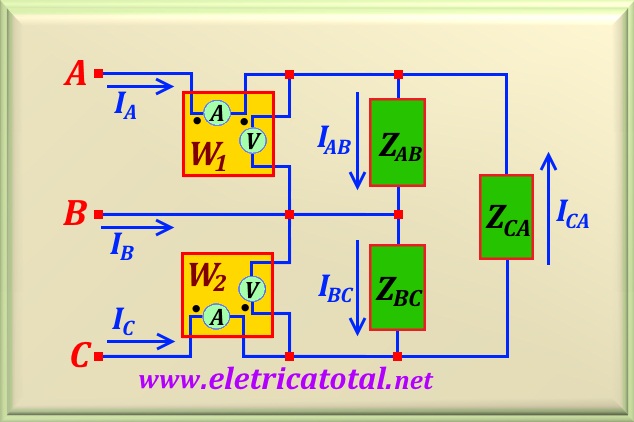
No circuito mostrado na Figura 85-03.1, V_AB = 208∠0°, V_BC = 208∠-120°, V_CA = 208∠120°, Z_AB = 10 Ω, Z_BC = 15 + j20 Ω e Z_CA =12 - j12 Ω. Essa carga não-equilibrada, conectada na configuração delta, possui dois wattímetros ligados conforme circuito mostrado na Figura 85-03.1. Encontre:

a)  o módulo e o ângulo das correntes de fase.

b)  o módulo e o ângulo das correntes de linha.

c)  a leitura dos wattímetros.

Solução do Problema 85-3

Item a

Para se calcular a corrente de fase, I_AB, basta aplicar a lei de Ohm. Assim:

Para o cálculo de I_BC, deve-se passar o valor da impedância da fase correspondente para a forma polar, ou Z_BC = 15 + j20 = 25∠53,13°. Então:

Para o cálculo de I_CA, Z_CA = 12 - j12 = 16,97∠-45° . Então:

Item b

Para se calcular as correntes de linha, aplica-se a lei de Kirchhoff a cada nó do circuito. Assim:

Para se calcular I_B:

E para I_C:

Efetuando-se o cálculo:

Item c

Para o cálculo das leituras dos wattímetros, deve-se prestar muita atenção no ângulo de defasagem entre a tensão e a corrente que o wattímetro lê. No caso de W₁, ele está lendo a corrente I_A e a tensão V_AB. Como V_AB tem ângulo zero e a corrente I_A possui um ângulo de 5,55°, então a defasagem entre elas é de 5,55°. Logo, a leitura de W₁ será:

No caso de W₂, ele está lendo a corrente I_C e a tensão V_CB. Repare que a tensão fornecida foi V_BC que está defasada de 180° em relação a V_CB. Então, o ângulo de V_CB será -120° +180° = 60°, ou seja, a defasagem entre a corrente e a tensão é de 130,65 -60° = 70,65°. Logo, a leitura de W₂ será:

Note que não se levou em consideração o sinal do ângulo de defasagem entre a tensão e a corrente, pois se sabe que cos (- φ) = cos φ.