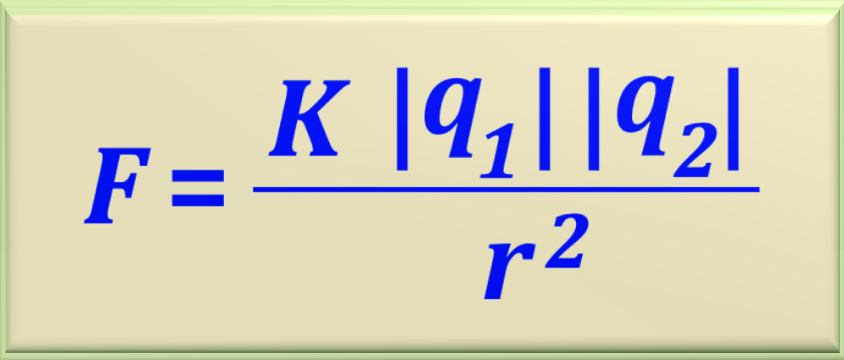Problem 71-2    Source:  Problem developed by the author of the site.

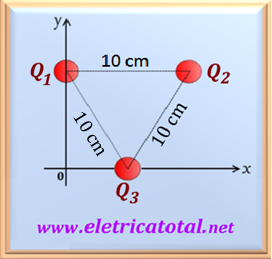
We see in Figure 71-02.1 the distribution of three particles, Q₁, Q₂ e Q₃, in the x-y plane. If the three particles have the same charge, being equal to + 5 µC, calculate the force, in module and direction, that the particle Q₃ suffers in the presence of the other two.

Solution of the Problem 71-2   

Since all particles have charges of the same polarity, then the forces will be repulsive. For the calculation of the modulus of forces, we will use eq. 71-04, studied in item 3 of chapter 71 and repeated here for clarity.

Let's calculate the force that the Q₁ particle exerts on the Q₃ particle, representing this force by F_1-3. Remembering that K = 9 x 10⁹ N . m² / C². Assim

Performing the calculation we find the force module, or

As the Q₁ and Q₂ particles are at the same distance from the particle Q₃, then the values of the modules of the two forces will be equal. Changes only the direction as we can see in the Figure 71-02.1.

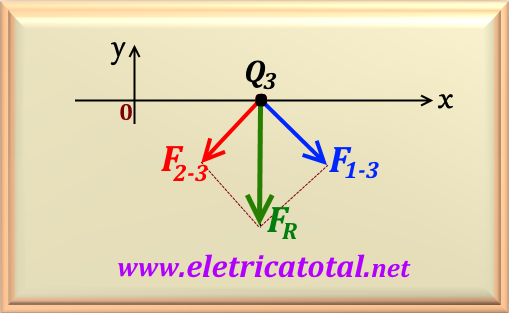
Note that to find the resultant force value on the particle Q₃, we must add vectorically the forces F_{1- 3} and F_2-3. However, from Figure 71-02.2 we realize that the angle between these two forces is equal to 60°, since the three particles are located at the vertices of an equilateral triangle. Then we can calculate the value of the resulting force using the eq. 51-02, studied in chapter 51 and we will repeat it here to remember a very important equation.

In this equation, we have to x = F_R, a = F_1-3, b = F_2-3 and φ = 60°. Then, making the numerical substitution and performing the calculation, we obtain:

This is the modulus of the resulting force. As for the direction and direction we can see from Figure 71-02.2 that has direction and direction of the negative y-axis . Vectorally, we can write it as