Problem 71-11
Source: Entrance Exam PUCRJ - RJ - 2009.
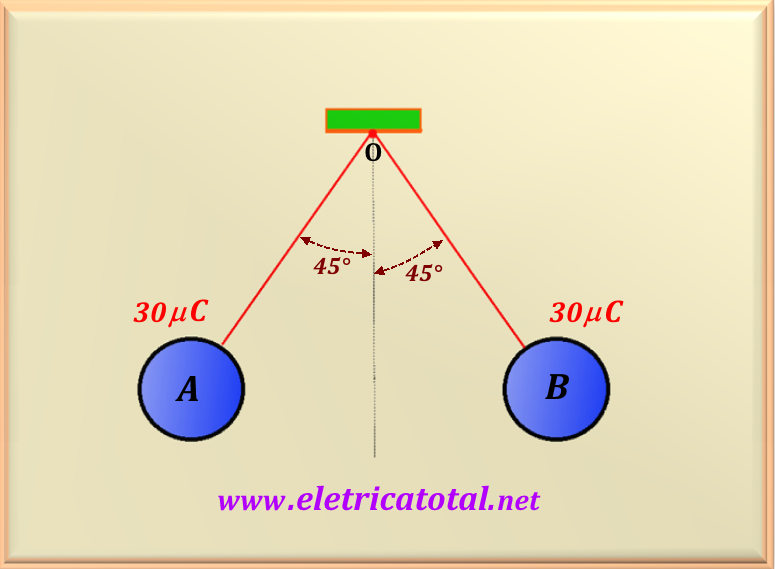
Two identical spheres, charged with charges Q = 30 µC, are suspended from
from the same point by two insulating wires of the same length as shown in Figure 71-11.1.
In balance, the angle formed by the two insulating wires with the vertical is 45°.
Knowing that the mass of each sphere is m = 1 Kg and considering the Coulomb constant
K = 9 x 109 N m2/C2, determine the distance between the two
spheres when in balance. Consider g = 10 m/s2.
Solution of the Problema 71-11
The Figure 71-11.2 shows the scheme of the forces acting on the B sphere and the
problem data we know that θ = 45°. As the spheres have the same polarity
there will be an electrical repelling force between them. The wire tension can be decomposed
into two components: one on the x axis, like T senθ and one on the y axis,
like T cosθ. And on the y axis, pointing down, we have the weight force,
PB.
Knowing that m = 1 Kg, we have PB = m g = 10 N.
Since the system is in equilibrium, the algebraic sum of forces on the y
axis must be equal to zero. Then, the tension in the wire can be calculated using
Doing the same for the y axis, we find
We now have all the data needed to calculate the distance between the spheres.
For this we will use Coulomb's law, according to eq. 71-04.
After an algebraic arrangement in the equation, we have
Substituting the numerical values and performing the calculation, we find
So, extracting the square root, we get