Problem 71-10
Source: Proof 1 - IFSC - SC - 2011.
An electric pendulum of length R and mass m = 2 Kg electrified with a
positive charge Q, is repelled by another equal charge, fixed at point A.
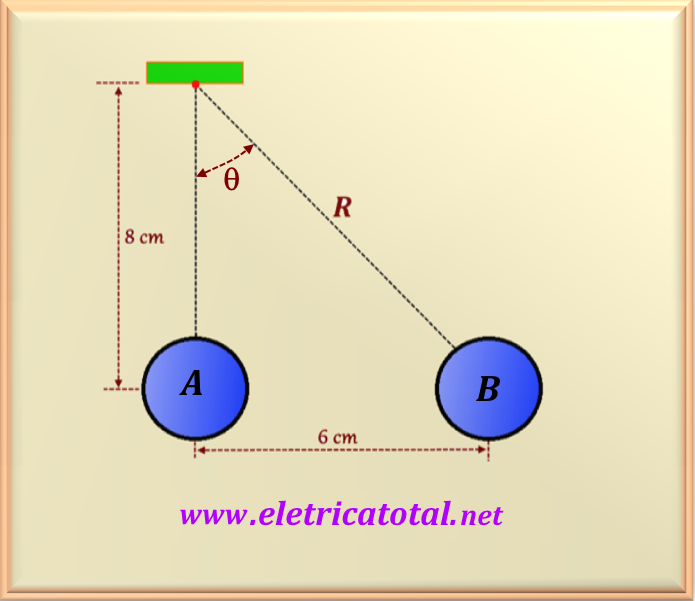
The Figure 71-10.1 shows the equilibrium position of the pendulum.
Considering g = 10 m/s2 , find the charges module.
Solution of the Problem 71-10
From Figure 71-10.2 , we quickly discover the value of R = 10 cm, because for that
just apply the Pythagorean theorem to the triangle formed by the distances shown in the figure.
On the other hand, by applying a little trigonometry to this triangle, we will be able to determine the value of
cosθ = 8/10 = 0.8 and, consequently, senθ = 6/10 = 0.6.
With this data, we will determine the value of the tension in the wire supporting the load B ,
remembering that its weight is equal to PB = m g = 2 x 10 = 20 N.
As the system is in equilibrium, the sum of the vertical and horizontal forces must be
equal to zero. Note that vertically, we can write that:
Substituting for the numerical values and performing the calculation we find the tension
over the wire, or
Now, analyzing the horizontal we see that there is a T senθ force that tries to
bring the two loads together. As the problem says that the system is in balance,
then there must be a repelling electrical force pointing to the right to balance the system.
Writing the equation, we have:
But, we know that the electrical force between two charges is given by the law of Coulomb.
So, matching the found value of FE and remembering that the value of the
charges are equal, we get:
Substituting the numerical values and performing the calculation, we obtain: