Problem 55-10    Source:   Problem 13 - List of RLC Problems - Discipline Electrical Circuits of the School of Engineering - UFRGS - 2017 - Prof. Dr. Valner Brusamarello.

Determine V_ab in module and phase according to the circuit shown in the Figure 55-10.1.

Solution of the Problem 54-10   

Note that it is possible to calculate the impedance of the 1-to-2 branch by adding the values ​​of the components, as they are connected in series. Therefore, the impedance will be:

Thus, knowing the impedance we can calculate the value of I₁, or:

Performing the calculation:

Note that the impedance between the point 1 and the point a is Z_1a = 9 - j12 = 15∠-53.13°. In this way, we can calculate the voltage between the point 1 and the point a, or:

On the 1-b-2 branch, note that the impedance between points 1-b and b-2 are exactly the same regardless of the values of R and X<. This implies that V_1b = V_b2. And since the source voltage is V = 100∠0°, it is concluded that:

To find the value of V_ab just make the upper mesh, or:

Performing the numerical substitution and calculating:

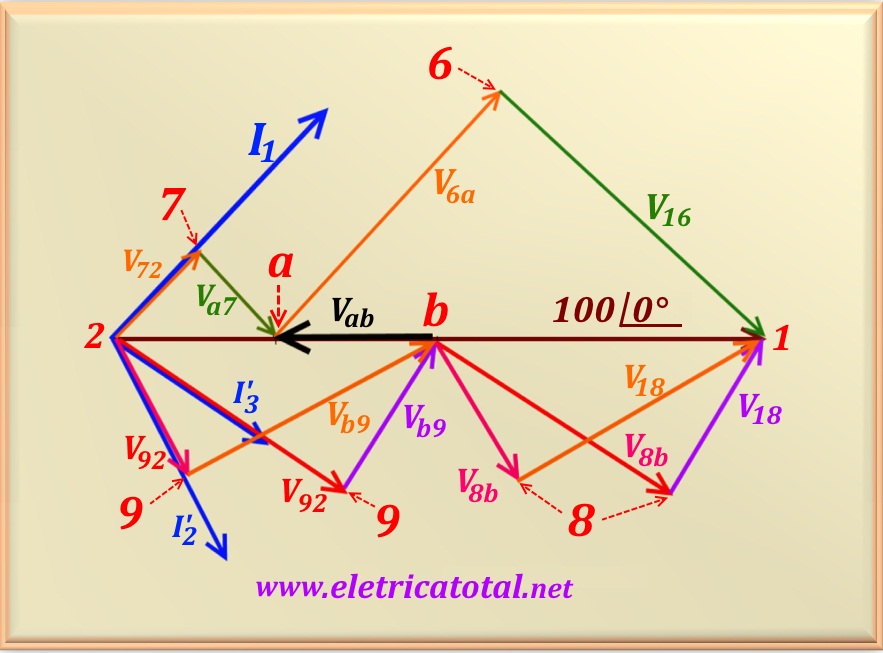
In the Figure 55-10.2, we present a phasor diagram of the voltages and currents in the circuit. Notice that the phasors that are above the reference voltage correspond to the branch containing capacitors. Analyzing the branch that is between the points 2 and a: note that the voltage V₇₂ is in phase with current I₁ and is the voltage on the 3 ohm resistor; the voltage V_a7 is the voltage on the capacitor -j3 and is delayed by 90° in relation to the voltage on the resistor, V₇₂; the phasor sum of these two voltages is the voltage V_a2. Now let's look at the branch that is between the points a and 1: the voltage V_6a is the voltage across the 9 ohms resistor and is in phase with I₁ as can be seen in the diagram; the voltage V₁₆ is the voltage across the capacitor and is delayed by 90° in relation to the voltage across the resistor, V_6a; the phasor sum of these two voltages is the voltage V_1a, whose value has been calculated and is equal to V_1a = 75∠0°.

Now let's make an analysis of the part that is below the reference voltage and, in this case, analyzing the branch containing the inductors. To be clear that the solution of the problem is independent of the values of R and X_L, we chose to represent two currents, I'₂ and I'₃, with different phase angles, which means two different values for R and X_L. Note that in the case of I'₃, results V₉₂ > V_b9, then R > X_L. And to I'₂, results V₉₂ < V_b9, then R < X_L. It is then verified that, for any values of R and X_L the same solution is obtained for V_ab. See, in the diagram, V_ab pointing in direction contrary the voltage of the power supply. This justifies the value found V_ab = -25∠0° = 25 ∠180°   V.