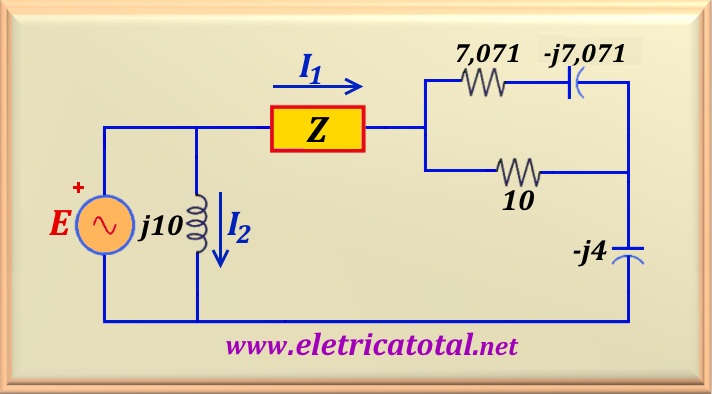
Problem 55-11    Source:   Problem 16 - List of RLC Problems - Discipline Electrical Circuits of the School of Engineering - UFRGS - 2017 - Prof. Dr. Valner Brusamarello.

In the circuit shown in the Figure 55-11.1 |I₁| = |I₂|. Knowing that I₁ is advanced 90° in relation to I₂, determine the value of Z.

Attention: In the UFRGS list there is a mistake typo in the result of the value of X_L. The correct value is jX_L = +j1.93 and not   5√2 - 1.

Solution of the Problem 54-11   

Since the phase of the voltage source was not supplied, we choice E∠0°. In this way, the current I₂, which circulates through the inductor j10, is delayed by 90° in relation to the source E. By the statement of the problem, I₁ is 90° advanced in relation to I₂. This means that I₁ is in the same phase as the voltage source E∠0°. In this way, the whole circuit that is between the points d , e and c, when added to Z, should result in pure resistance. Calculating the equivalent impedance between points d-e, called Z_de, there is the parallel of the 10 ohms resistor with the impedance 7.071 - j7.071 = 10∠-45°, that is:

At this value, adding the capacitor -j4, we obtain:

On the other hand, by the statement of the problem, it is known that |I₁| = |I₂|. For this, we must have Z_adec = 10 ohms, that is, the same reactance of the inductor. Like this:

Performing the calculation:

Therefore, the impedance Z must be a series circuit consisting of a resistor with a value equal to 5 ohms and an inductor with inductive reactance equal to 1.93 ohms. This inductive reactance cancels the capacitive reactance of Z_dec and as a result, there will be a resistance of value equal to 5 + 5 = 10 ohms in parallel with the inductor j10.