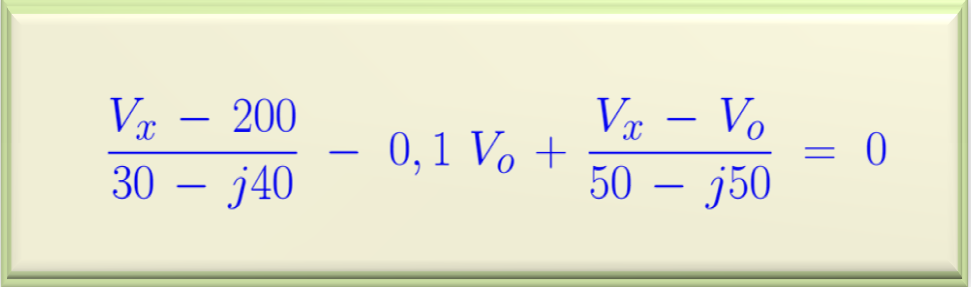Problem 53-7    Source:  Problem prepared by the site's author.

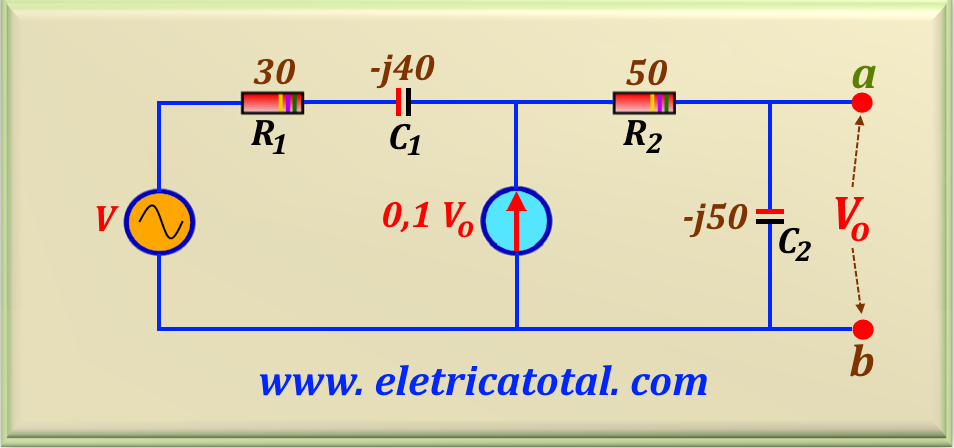
In Figure 53-07.1 we have V = 200∠0°. Determine the Thévenin equivalent of the circuit from the point of view of the terminals a - b.

Solution of the Problem 53-7

To determine the Thévenin voltage it is necessary to calculate the open circuit voltage at the terminals a - b. To do so, we will apply the nodal voltage method to the node x. We will call the voltage at this point V_x. So, we can write the following relationship:

Note that from the circuit we can determine a relationship between V_o and V_x using a voltage divider, i.e. :

Substituting eq. 53-07.2 in eq. 53-07.1 let's find the value of V_x, or:

Therefore, substituting this value in eq. 53-07.2 we will find the value of V_o which is the Thévenin voltage itself. Then

Now to calculate the Thévenin impedance we must put the terminals a - b in short circuit and calculate the current passing through the short circuit. Let's call this current I_sc. Note that by short-circuiting terminals a - b we will obtain V_o = 0, so the dependent source will be an open circuit and the capacitor C₂ will be shorted. They will soon be eliminated from the circuit. So, I_sc is equal to:

Now we are able to calculate the Thévenin impedance, because:

Carrying out the calculation, we obtain:

The impedance Z_th can be represented by a series circuit between a resistor with a value equal to 44.7 Ω and an inductor that presents a inductive reactance of 18 Ω.