Problem 11-7 Source:
Problem 34 - page 114 - HAYT, William H. Jr. ,
KEMMERLY, Jack E. , DURBIN, Steven M. - Book: Análise de Circuitos em Engenharia -
Ed. McGraw Hill - 7ª Edição - 2008.
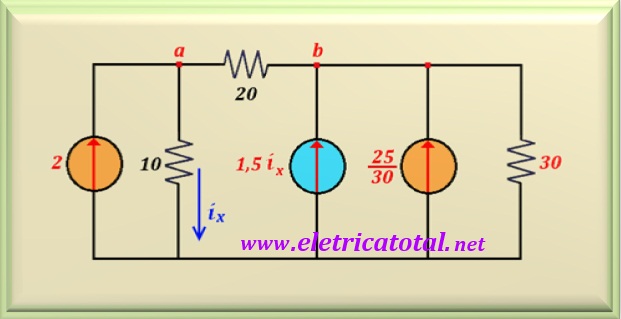
In the circuit show in Figure 11-07.1, calculate the current ix.
Solution of the Problem 11-7 -
Method of Transforming Sources
Let's start our analysis by doing a source transformation on the right side of the
figure above. The transform will be between the current source of 5A and the
5 ohms resistor that is in parallel with it. This will result in a voltage
source of 25 volts. The resistor of
5 ohms will be in series with the other resistors of the circuit, whose value
is 25 ohms.
Since the two will be in series then we can sum their values resulting in a resistor
of 30 ohms in series with the voltage source of 25 volts.
In this way, we can make a new transformation resulting in a current source
of 25/30 A in parallel with the resistor of30 ohms.
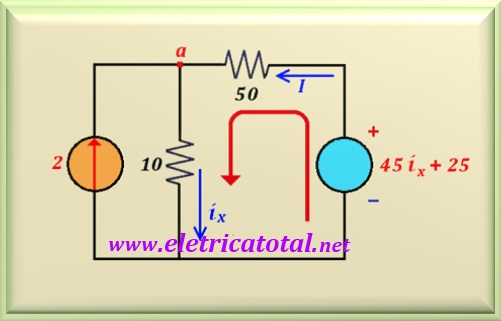
In the Figure 11-07.2 we redesign the circuit with the applied transformations.
As the two sources of current point in the same direction we can add them. Then we get a current source of value equal to 1.5 ix + (25/30).
Performing a further transformation of sources we find a voltage source of 45 ix + 25 .
The resistors of 20 Ω and 30 Ω are in series and can be
replaced by a single one of 20 + 30 = 50 Ω, resulting in the circuit
according to the Figure 11-07.3.
Notice that we call the current that flows through the 50 ohms resistor
of I. Therefore, from the circuit we can write that:
By making the mesh equation in the direction of the red arrow, indicated in the
figure above,
we obtain the following equation:
Substituting the value of I in this last equation, we easily find the value of
ix, whose value is: