Problem 13-2    Source:    Problem elaborated by the author of the site.

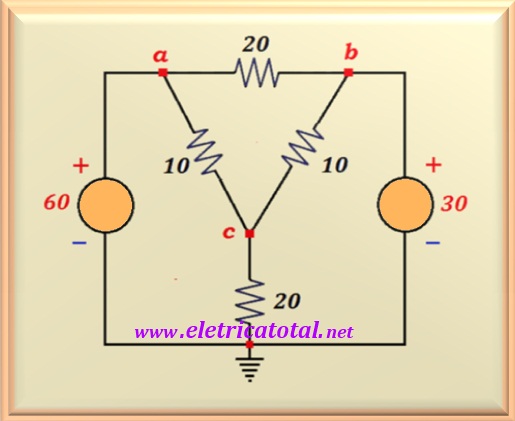
For the circuit shown in the Figure 13-02.1, calculate:

a) The currents that circulate in the circuit.

b) Make a power balance of the circuit.

Solution of the Problem 13-2   -    Kirchhoff Method

Item a

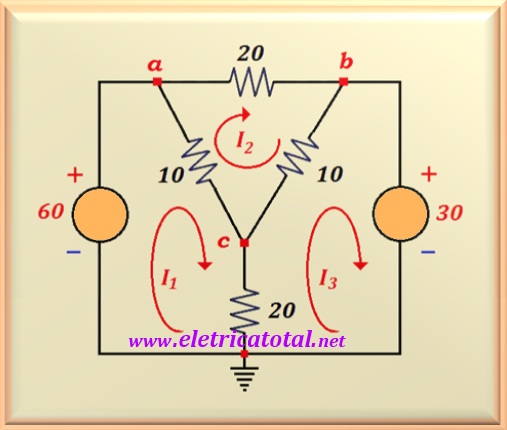
By the law of Kirchhoff for voltage we know that in a closed loop the algebraic sum of the voltages must be equal to ZERO . In the Figure 13-02.2 we see the redesigned circuit where shows the currents I₁ , I₂ and I₃.

We can write the three equations for the three meshes of the circuit, obeying the clockwise direction of the currents. See, below, the system of equations that will allow solve the circuit.

Therefore, we have a system of three equations with three unknowns. After calculations we find the values of the currents, or:

With these values, we can calculate the currents that pass through the circuit.

I) The current through the 20 ohms resistor that is between the points a and b, it's the current itself I₂ = 1.5 A.

II) The current through the 10 ohms resistor that is between the points a and c, is the difference between I₁ and I₂, that is, 2.4 A.

III) The current through the 10 ohms resistor that is between the points b and c, is the difference between I₂ and I₃, that is, - 0.60 A. This means that the current flows from the point c to the point b .

IV) The current through the 20 ohms resistor that is between the point c and the ground, is the difference between I₁ and I₃, that is, 1.80 A.

Now we can calculate the currents that circulate through the voltage sources using the law of Kirchhoff to the nodes. Recalling that we consider positive the currents that they leave the node and negative the currents that arrive at the node. Then we have:

For the voltage source of 30 volts , we have:

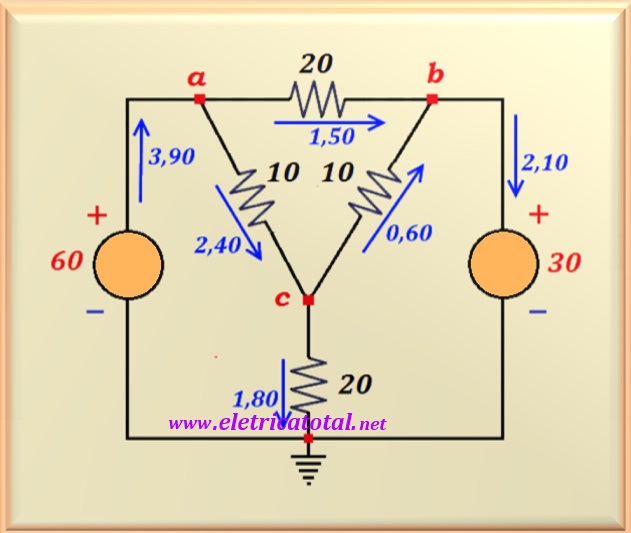
In the Figure 13-02.3 we can appreciate the circuit and the indication of all the currents through the various elements of the circuit.

Notice that at the voltage source of 60 volts , the current of 3.90 A exits by the positive pole and therefore it is the supplier of all energy consumed by the circuit. Therefore, its power is negative . However, the voltage source of 30 volts consumes power since the current of 2.10 A enters the positive pole. And the resistors that compose the circuit also consume power. By doing a power balance this will be confirmed.

Item b