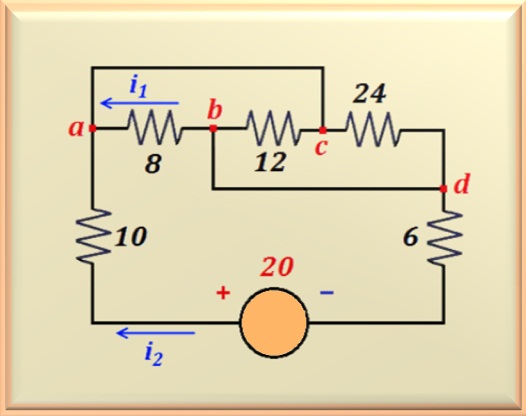
Problem 10-4 Source:
Problem elaborated by the author of the site.
On the circuit show in Figure 10-04.1, determine:
a) The currents i1 and i2.
b) What is the power dissipated in the 10 ohm resistor?
Solution of the Problem 10-4
Note that the 6 and 10 ohms resistors are in series. Therefore,
adding their values results 16 ohms.
In this circuit the greatest difficulty is to understand what kind of connection
we have with
the resistors that lie between the points a-b-c-d. To understand
circuits similar to this, the best decision is to give "names" to the nodes.
In our case,
we've already done that. Now just put the dots on paper and turn on the resistors
which make up the circuit according to the nodes. See the Figure 10-04.2, right side, as it was
the transformation of the circuit taking into account that the points a-c
are short-circuited, as are the points b-d.
From the figure above it is already possible to redesign the circuit and from
there calculate the currents
that the problem calls for. The Figure 10-04.3 illustrates the transformed
circuit. Note that the three resistors, in fact, are in parallel. Therefore,
the equivalent resistance value can be found
this parallel. After calculation, the value is Req = 4 ohms .
Finally, in the right-hand circuit, we see the simplification we could do to
compute current i2.
The parallel of the three resistors has been replaced by
Req = 4 ohms.
Applying the Ohm law, it's possible calculate i2, or:
Wih the value of i2 and looking at the circuit above, left side,
easily calculate the value of i1, it is sufficient to apply a
current divider. Note that i1 is pointing in the opposite direction to
i2. Then its value will be negative indicating that the correct direction is opposite to that represented in the circuit. Like this:
To calculate the power dissipated in the 10 ohms resistor, you must know the current flowing through it. As already calculated, the current i2 = 1 A. Then the power is: