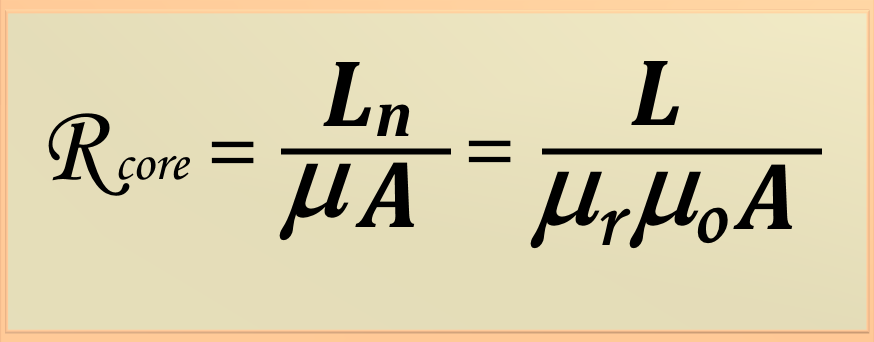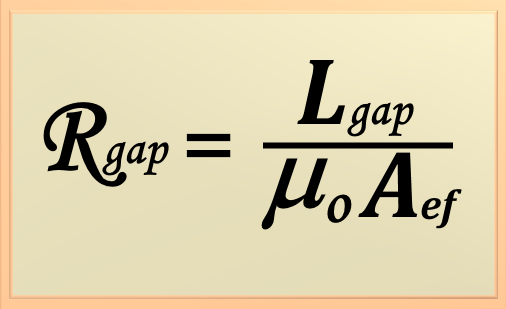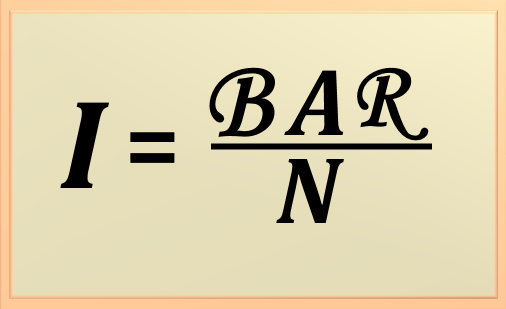Problem 77-4    Source:   Example 1-2 - page 17 - CHAPMAN, Sthephen J, - Book: Fundamentos de Máquinas Elétricas - 5ª edição - Ed. McGraw-Hill - 2013.

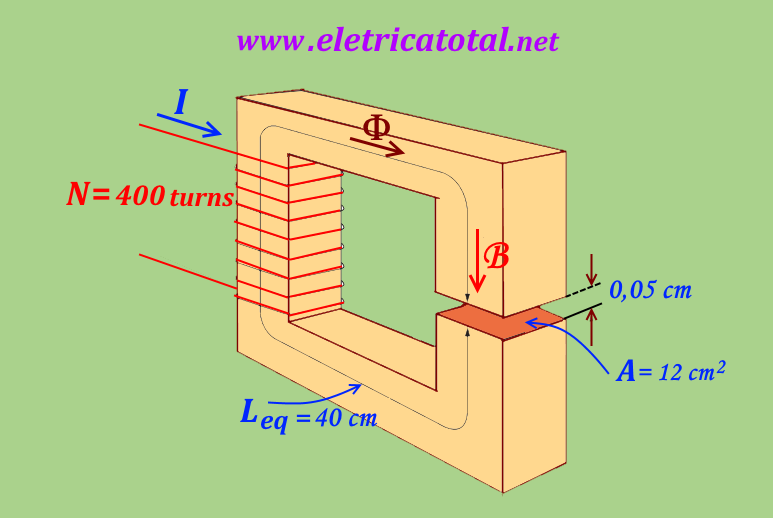
A ferromagnetic core is shown in Figure 77-04.1 whose average path length is 40 cm. There is a thin air gap of 0.05 cm in the core, which is solid in the rest. The area of the straight section of the core is 12 cm², the relative permeability of the core is 4 000 and the coil wound around the core has 400 turns. Assume that the spread in the air gap increase the effective area of the straight section by 5%. Given that information, find:

a) the total reluctance of the flow path (iron plus air gap).

b) the current required to produce a flow density of 0.5 T in the air gap.

Solution of the Problem 77-4   

Item a   

For the calculation of magnetic reluctance we will use eq. 77-18, repeated below:

Replacing with numeric values

Carrying out the calculation, we have

This is the value of the reluctance in the ferromagnetic part of the core. Now let's calculate the reluctance at the core air gap.

The effective area of the core in the air gap is A_ef = 1.05 x 12 = 12.6 cm². Therefore, the reluctance in the air gap, R_gap, is given by

Making the numerical substitution of the values we have:

Carrying out the calculation, we have

Now we can calculate the total reluctance that the core path offers to the magnetic flux, that is:

After substitution by numeric values and performing the calculation:

Item b   

From eq. 77-13 we know that F = ΦR  and beyond that, Φ = BA e F = N I. Relating these equations, we find that N I = BAR . And so, we arrive at the following equation:

Substituting for numeric values, we have

Carrying out the calculation, we find

As the problem asks for the determination of the current in the air gap so that we have a flow density of 0.5 T , then we use the effective area of the air gap.