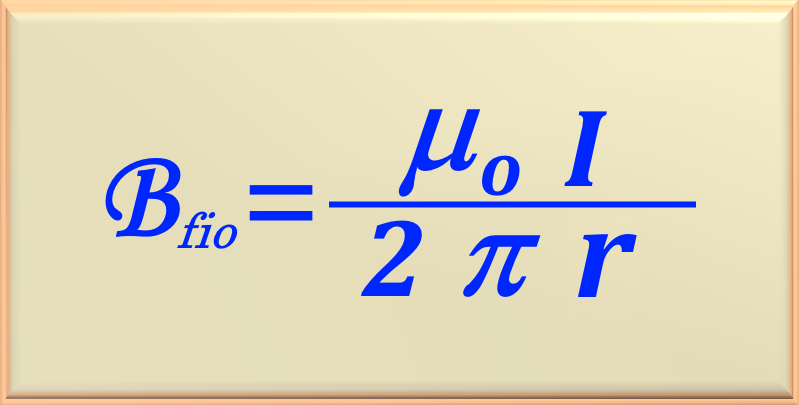Problema 74-7    Source:   Adapted from the example 22.8 - page 162 -    SERWAY, Raymond A. - Book: Princípios de Física - Vol 3 - Ed. Cengage Learning - 5ª edição - 2014.

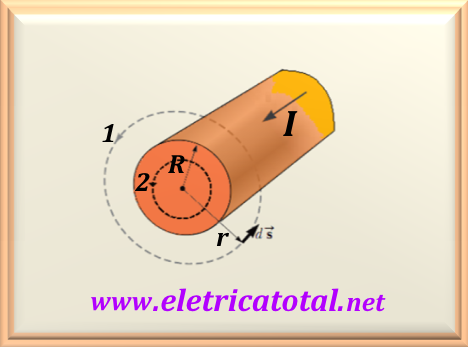
Let it be a long, straight wire with a radius of R = 1 cm and being traversed by a stationary current equal to I = 100 A , evenly distributed across the cross section of the wire , according to shows Figure 74-07.1 . Determine:

a) the magnetic induction field at a distance r = 0.5 cm.

b) the same calculation considering r = 1.5 cm.

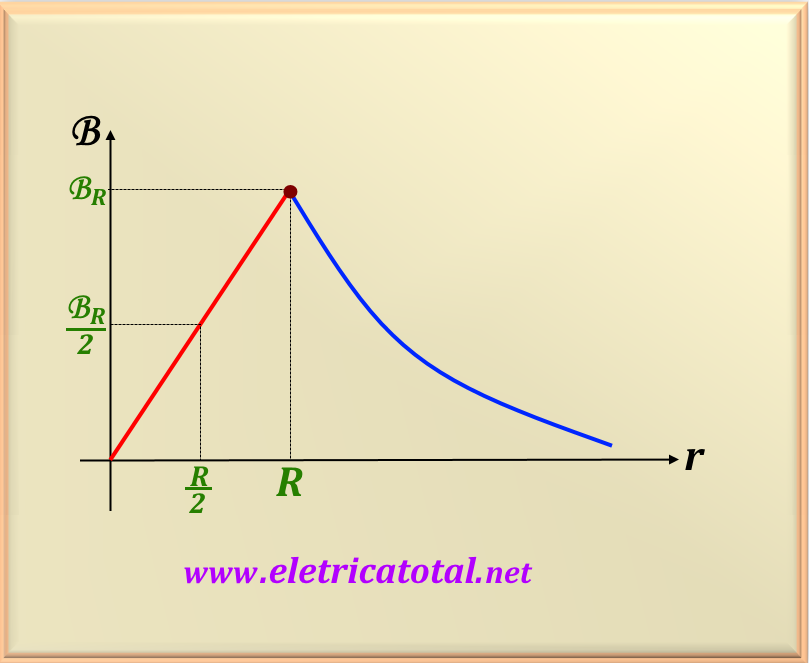
c) show in a graph the behavior of B as a function of r.

Solution of the Problem 74-7   

Item a   

Based on symmetry, it is possible to solve this problem using Ampère's law. For the case of r > R, the current passing through the amperian (plane of circle 1 in Figure 74-07.1) is the total current value, that is, I = 100 A. In this case, we can apply eq. 74-24, repeated here for a better understanding of the solution.

So, as r = 1.5 cm = 1.5 x 10^-2 m and replacing in eq. 74-24, let's get:

Carrying out the calculation, we obtain:

Item b   

For the case where r < R , we must define the amperian (in this case, we choose the plane of circle 2 in Figure 74-07.1) and then calculate the current that passes through the amperian. For this we will consider a current I' circulating inside circle 2 and making the proportion between the areas we will find:

Substituting for the numerical values, we find

Now that we know the current value, just replace the values in the eq. 74-24.

Performing the calculation, we obtain:

Item c   

In the Figure 74-07.2 we see the graph of the behavior of the magnetic induction field inside and outside the wire. Note that inside the wire the magnetic induction field is directly proportional to r , while outside the wire it is inversely proportional, that is, 1/r.