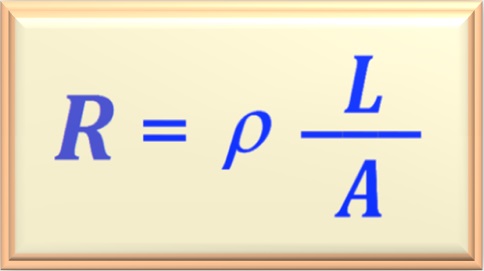Problem 73-5  Source:   Problem developed by the author of the site.

In the Figure 73-05.1 we see an electrical cable used in high voltage transmission lines. Notice the core made of a special carbon compound of radius a, being more resistant and light than steel and non-conductive. The conductive material is aluminum with external radius b. This cable has a rated current of I = 1.00 kA.

a) If a = 4.5 mm and b = 14.5 mm, find the current density.

b) Calculate the Ω/Km ratio of the cable

c) Find the Joule loss of the cable per Km for the rated current.

Solution of the Problema 73-5   

Item a   

To calculate the current density we must calculate the cable area. So, let's calculate the cable area considering the external radius b and then subtract the area considering the internal radius a. Soon:

Performing the calculation we find the area value, or

Having this data and using the eq. 73-06, we calculate the current density, or

Turning this value to A/mm² , we will find J = 1.67 A /mm². Comparing with the current density used in transformer projects, which can vary from 1.50 to 3.00 A /mm², depending of the use of the transformer, we realize that the value found for the transmission line is a very pertinent value.

Item b   

To calculate the ratio Ω/km we must know the resistivity of aluminum. Consulting the Table 02-01 in Chapter 2, we have ρ = 2.75 x 10 ^-8 Ω . m . So, let's use the eq. 02-01 to calculate the electrical resistance of the cable when its length is L = 1 000 m . Below we reproduce the eq. 02-01, for clarity.