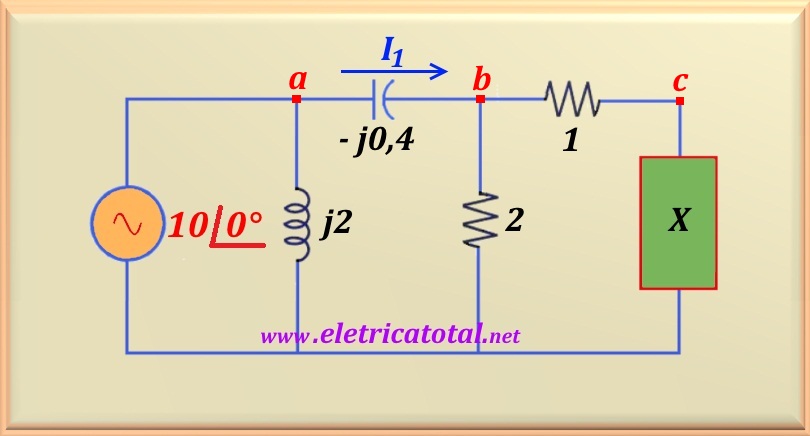
Problem 55-6    Source:   Problem 9 - List of RLC Problems - Discipline Electrical Circuits of the School of Engineering - UFRGS - 2011 - Prof. Dr. Valner Brusamarello.

In the circuit of the Figure 55-6.1 find the nature and values of X that make null the phase angle of current I₁.

Solution of the Problem 55-6   

Notice that the inductor j2, being in parallel with the voltage source can be eliminated from the circuit without prejudice to the solution of the problem. As the electric current I₁ passes through the capacitor of - j0.4, then it will be advanced in relation to the voltage V_ab. Therefore, the circuit to the right of the capacitor should delay I₁ so that it can get zero degree angle. The only passive element that can delay electrical current is the inductor. Therefore the element X is an inductor. This means that the circuit to the right of the capacitor must have an impedance of type R + j0.4, since the imaginary part j0.4 must cancel the capacitor reactance ( - j0.4). Soon:

Multiplying numerator and denominator by the conjugate complex of the denominator (technique of division of complex numbers), we find the expression:

Since interest is only in the imaginary part of the equation, discarding the real part, we obtain the equation below:

Then, the roots of this equation will be the admissible values for X. Then:

Therefore, it is possible to have two values for the inductor:   jX = j    or    jX = j9.