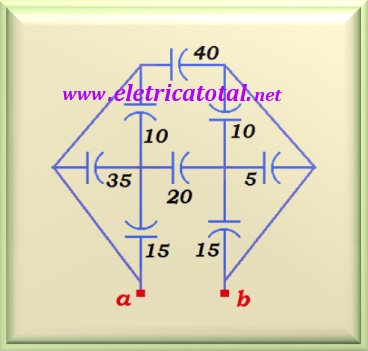
Problem 3.3 Source:
Problem 6.22 -
page 216 - SADIKU, Matthew N. O. , ALEXANDER, Charles K. -
Book: Fundamentos de Circuitos Elétricos - McGraw Hill - 5ª edição - 2013.
In the circuits shown in Figure 03-03.1, the cpacitances are given
in µF. Calculate the equivalent
capacitance between points a and b.
Solution of the Problem 3.3
Analyzing the circuit on the left side, we noticed that the capacitors
of values 15, 35 and 10 µF are in parallel, and are bound to
point a. Therefore, to calculate the equivalent capacitance of these
three capacitors just add their values, or:
Likewise, looking at the capacitors that are connected
to point b, we notice that they are also in parallel. Therefore, the
equivalent capacitance of these three capacitors will be its sum, or:
As we can see in the Figure 03-03.2, the circuit has been reduced to
a series-parallel combination of four capacitors. It's easy to see
that the capacitors of 60, 20 and 30 µF are in series.
Recalling the equation that allows us to calculate the capacitance
equivalent for three capacitors in series, we have:
Substituting for the numerical values, we find:
Therefore, we were able to reduce the circuit to two capacitors in parallel,
that after performing the calculations (adding the values of the capacitors) we
find the final value of: