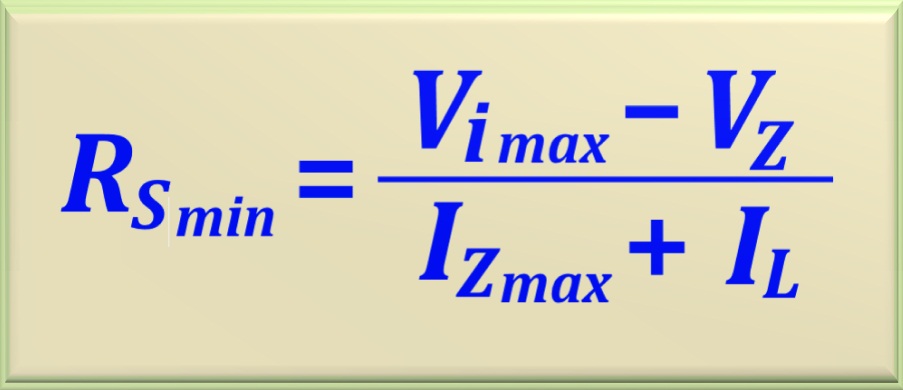Problema 64-3    Fuente:  Problema elaborado por el autor del sitio.

Sea el circuito que se muestra en la Figura 64-3.1. Suponiendo que Vi = 27 volts con ΔV = 4 volts y V_Z = 15 volts. La corriente consumida por la carga es 100 mA. Determinar los valores de R_Smax y R_Smin y cuál es la potencia en zener.

Solución del Problema 64-3   

Tenga en cuenta que el voltaje de entrada es variable pero la carga es constante. Entonces habrá variación en la corriente que fluye a través del zener. Por lo tanto, aplica el CASO 3 estudiado en el ítem Teoría . Dado que no se proporciona el modelo zener a utilizar, debe comenzar estipulando una corriente zener máxima. Como la carga consume 100 mA , se puede hacer la corriente máxima para el zener de, digamos, I_Zmax = 200 mA. En este caso, la potencia en el zener será:

Comercialmente no hay zener para esta potencia. El más cercano es 5 vatios. Así que supongamos que el zener es 5 vatios. Puede calcular cuál es la corriente máxima que puede transportar el zener o:

Entonces, I_Zmin será de:

Con estos dos valores, calculemos R_Smin e R_Smax utilizando las dos ecuaciones estudiadas. Vamos a repetirlos aquí.

Recordando que en este problema, V_i(min) = V_i - (ΔV/2) = 27 - 2 = 25 volts y para encontrar con la máxima, V_i(max) = V_i + (ΔV/2) = 27 + 2 = 29 volts. Entonces:

Y a su vez:

Nota que R_Smax > R_Smin haciendo viable el proyecto. Podemos elegir la serie de resistencia es el valor promedio de los valores calculados. Así, R_S = 54 ohms. Un valor comercial que se puede usar es R_S = 56 ohms

Tenga en cuenta que la corriente a través de R_S no es constante depende de las variaciones en el voltaje de entrada. Entonces tenemos I_Smax = (V_i(max) - V_Z) / R_S = 0,25 A . Por lo tanto, la corriente máxima que circula a través del zener es I_Zmax = (I_Smax - I_L) = 0,15 A . Entonces zener soporta esta corriente sin problemas. La potencia disipado por él será:

El uso de un 5 vatios zener no tendrá problemas de proyecto.